Signature

Introduction to the concept of Cross Entropy and its application

Oct 09, 2016

Topics covered:

  • Definition of Entropy

  • Explaination of Cross Entropy (KL Divergence)

  • Understanding how cross Entropy Loss function works with Softmax

  • 1

    What is Entropy?

    It is a measure of uncertainity.A Fair coin, for instance has highest Entropy, because heads and tails (outcomes) are equally likely.Entropy allows us to search for patterns in Big data.

    If we spin a wheel 10 times, what is the Entropy?

    Fig1:In the above graphic, probability is count of outcome (red or green or yellow) divided by total number of events. Log of this probability is the amount of information encoded as per Shannon's Information theory. Entropy for the above example is 1.5, which is measure of uncertainity. If Entropy is zero, there is no unertainity, that is it is easy to make predictions

    Another example to calculate Entropy of arrival times of an Airlines

    Download Excel sheet with Entropy calculations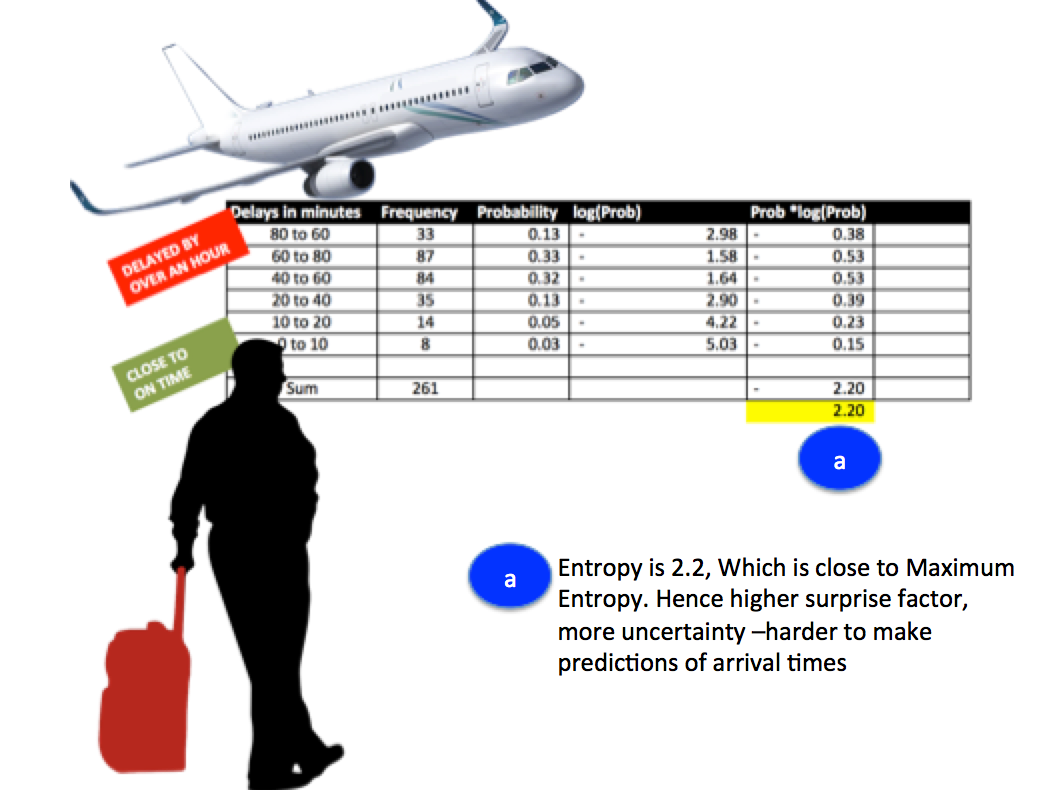

    Fig 2: In the visual, Arrival delays and their frequencies are listed. The goal is to asses the unertainity in data, which would enable prediction of delay in next arriving flight.Here Entropy is 2.2.The question would be how close is this measure of information to Max entropy(based on Shannon's Information theory) which is log to the base 2 of total number of outcomes.

    When is the Entropy Maximum in the sample Airlines delay data ?

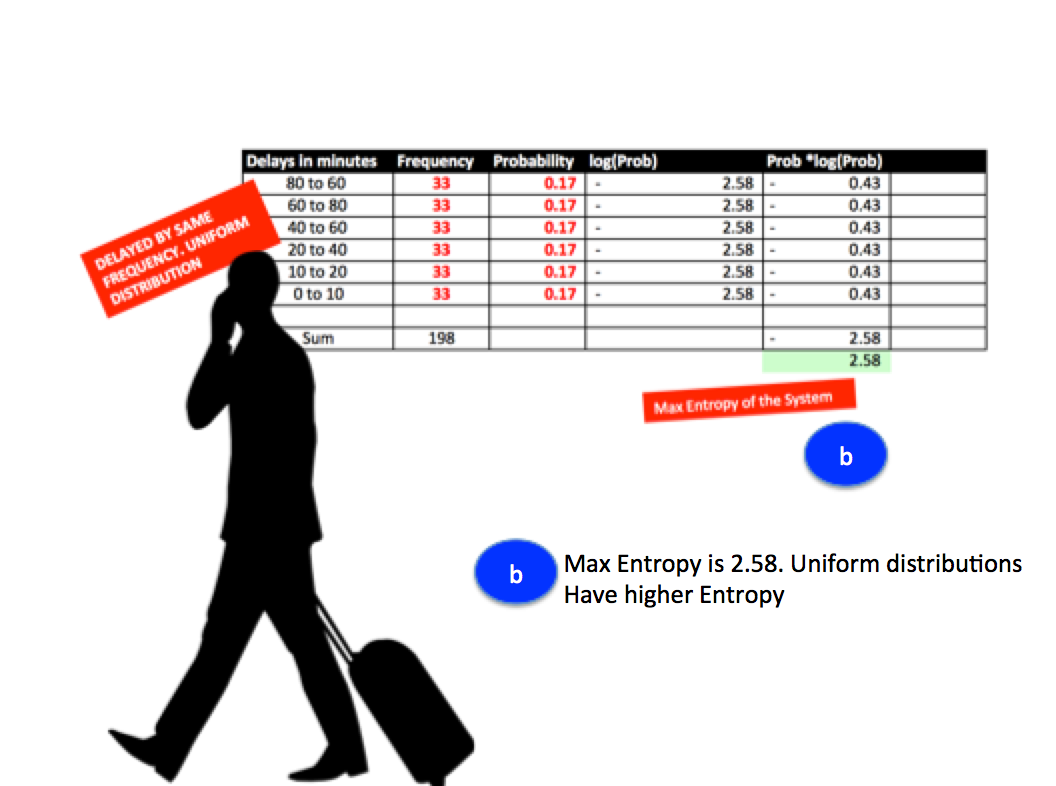
    Fig 3: When the frequencies are equally distributed, Entropy is highest. Calculated Entropy (2.2 from Fig2 ) is close to Maximum Entropy for the system (2.58), hence there is considerable uncertainty in the ability of this pattern to forecast delays. Higher Entropy suggests more patterns and higher uncertainity.

    • Reminder: If Entropy is high, surprise factor is high.Fair coin for instance has higher Entropy.Heads and Tails are equally probable

  • 2

    What is Cross Entropy ?

    In Machine Learning, Cross Entropy is used to compare approximate models.

    Lets assume we need to compare two arrival delay distributions taken during summer and winter seasons.

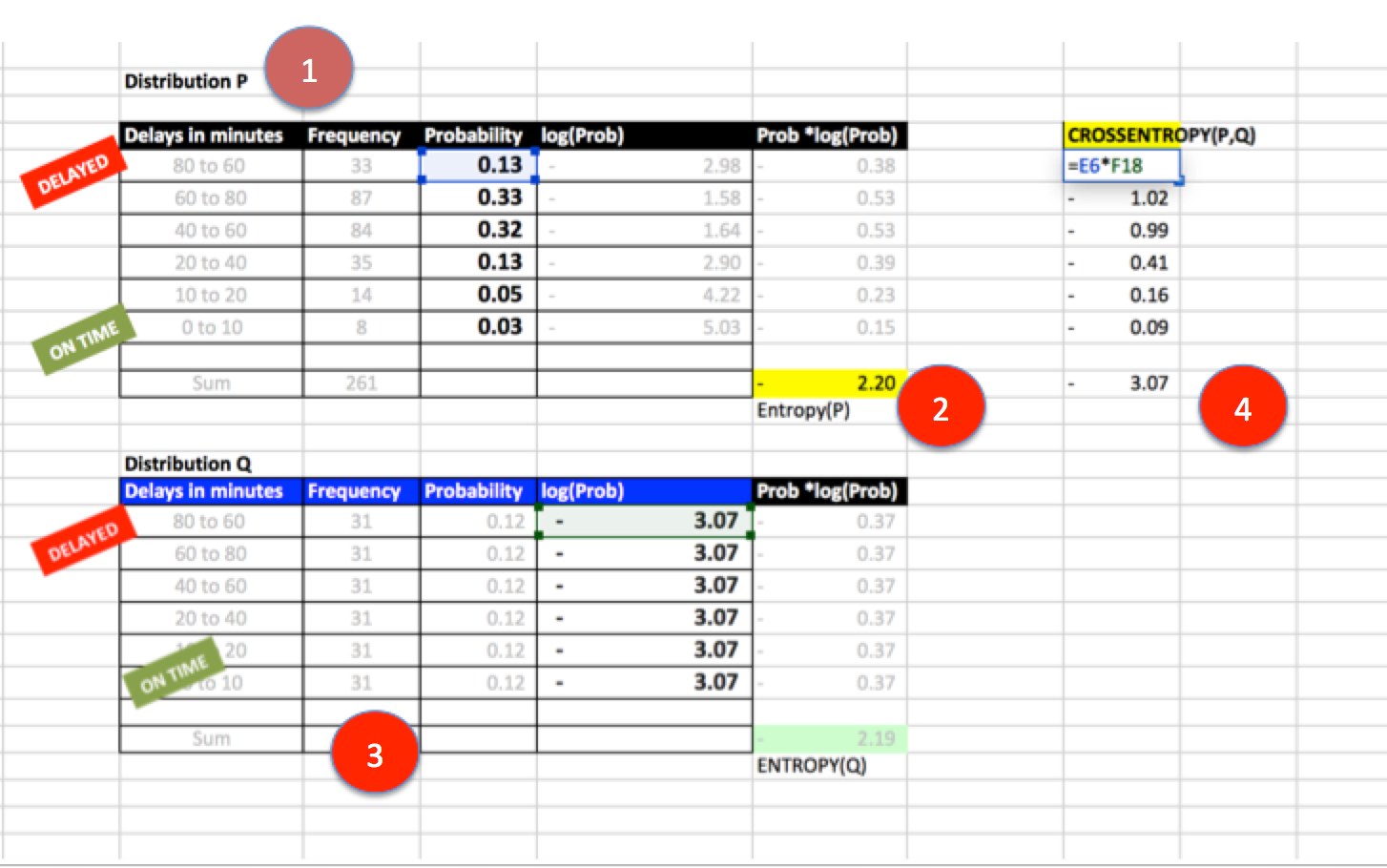
    • 1: Let this be a base reference distribution. Call it P.

    • 2: Note that Entropy for P is 2.2.

    • 3: Change these frequencies to form distribution Q

    • 4: Measure cross Entropy (P,Q)

    In the above example, cross Entropy(P,Q) is bigger than Entropy(P), hence P and Q are not good approimations.

    • Please note that KL Divergence is similar to Cross Entropy.Used to find distance between distributions

  • 3

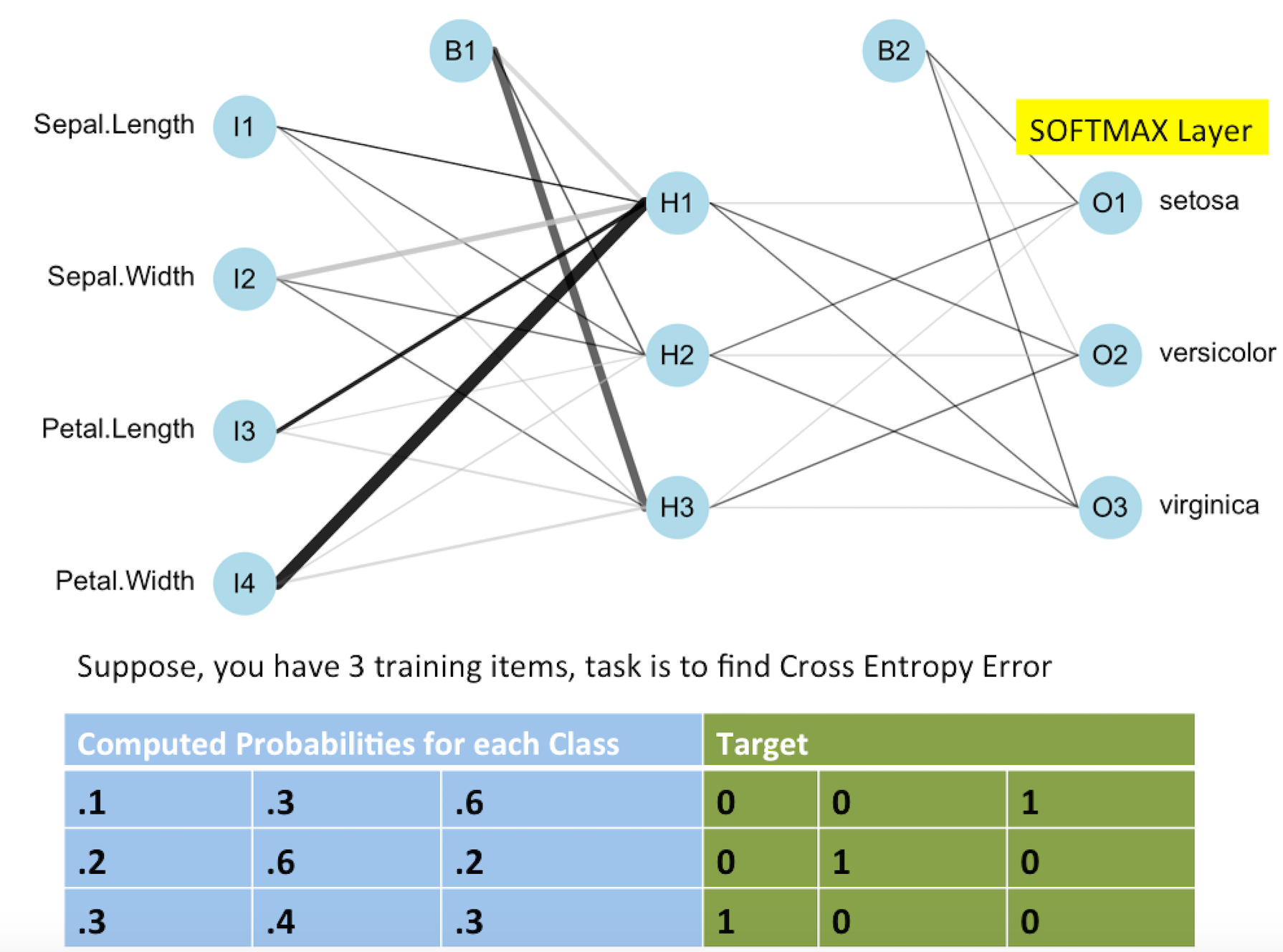
    Cross Entropy Loss function with Softmax

    • 1: Softmax function is used for classification because output of Softmax node is in terms of probabilties for each class.

    • 2: For The derivative of Softmax function is simple (1-y) times y. Where y is output

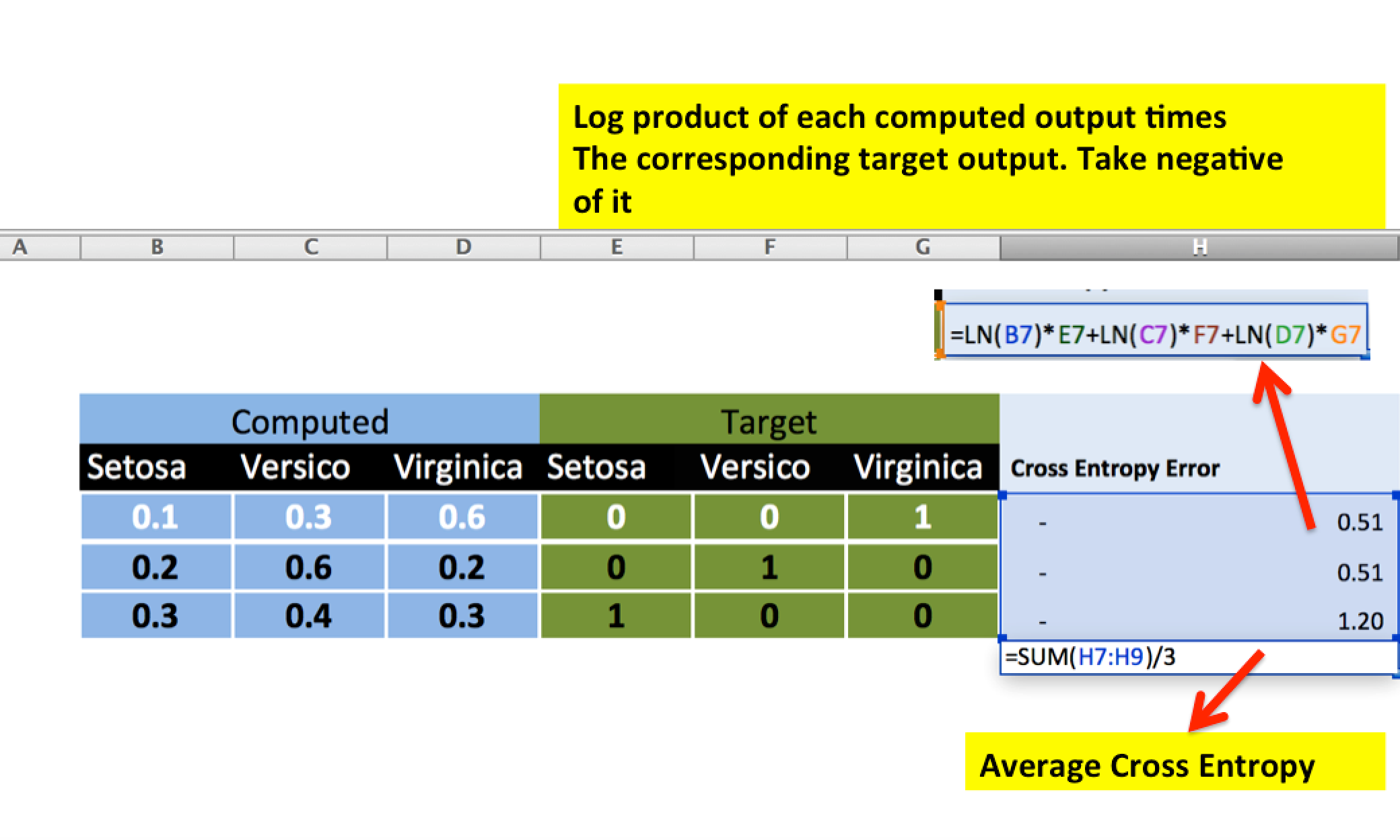
    • 3: Computation of gradients at each node is much easier with Softmax and Cross Entropy Error Function. Gradients at each is just the difference between target and computed output values

      • These gradients are a measure of how far off, and in what direction (positive or negative) the current computed outputs are relative to the target outputs.

      Watch Professor Hinton's explaination on benefits of using Softmax and Cross Entropy Loss function together for classification tasks

      Finally, code to plot neural net 

            library(neuralnet)
      library(NeuralNetTools)
      nnet_iristrain_1<-read.csv('https://dl.dropboxusercontent.com/u/75324587/data/neuralNet.csv')
      nn <- neuralnet(setosa+versicolor+virginica ~ 
                Sepal.Length+Sepal.Width
                            +Petal.Length
                            +Petal.Width,
                data=nnet_iristrain, 
                hidden=c(3))

       plotnet(nn, alpha=0.6)
    • Cross Entropy Example Derivative Cross Entropy

References

RExample clipArt Cross Entropy Example

  • BTW, you might also like these previous posts

Machine Learning Posts

Precision, Recall and F1 Score Secretary Problem. Strategy to select the Best Candidate A walk through Machine Learning Conference held at Toronto Introduction to the concept of Cross Entropy and its application Build a Neural Net to solve Exclusive OR (XOR) problem AI Winter. How Canadians contributed to end it? Perceptron Learning Algorithm in plain words Maximum Likelihood Estimate and Logistic Regression simplified Deep Learning highlights Month by Month Intuition behind concept of Gradient

Finance Posts

IPO Stocks Performance in 2019 S&P500 2018 returns Let's learn about Convertible Note SP500 Stocks Performance in 2017

General

Immense Power of Interactive Math Explainers

R/Python