Tweet

Though invented in 1960’s it is still used today, at places like Google. Why?

Here let us discuss:

Section1: Perceptron convergence

Before we dive in to the details, checkout this interactive visualiation of how Perceptron can predict a furniture category

Click here Pause

Visual #1: The above visual shows how beds vector is pointing incorrectly to Tables, before training. We shall use Perceptron Algorithm to train this system

Visual #2:This visual shows how weight vectors are adjusted based on Perceptron Algorithm.

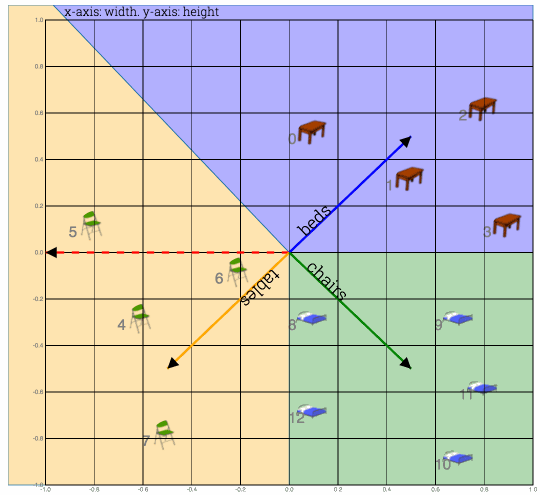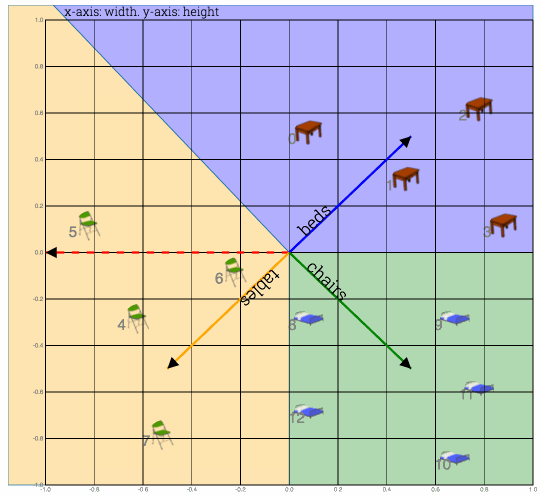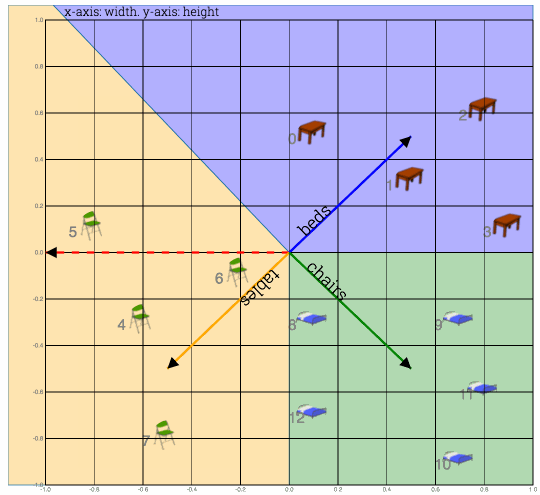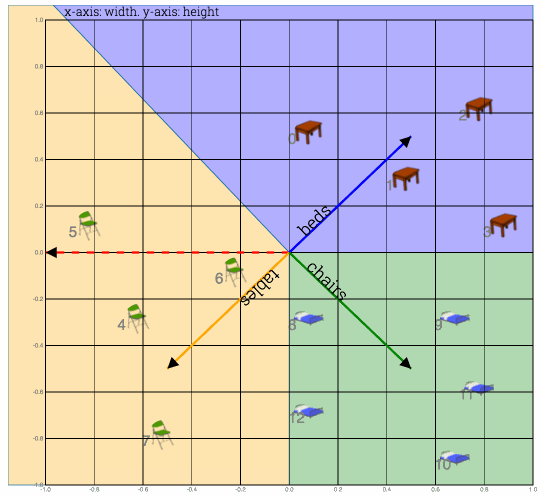
Notes: Walking through all inputs, one at a time, weights are adjusted to make correct prediction.If the classification is linearly separable, we can have any number of classes with a perceptron. Note that there is one weight vector for each class. Images from clker

Visual #3: Convereged state.

You might ask. Why are the axis in range -1 to 1?

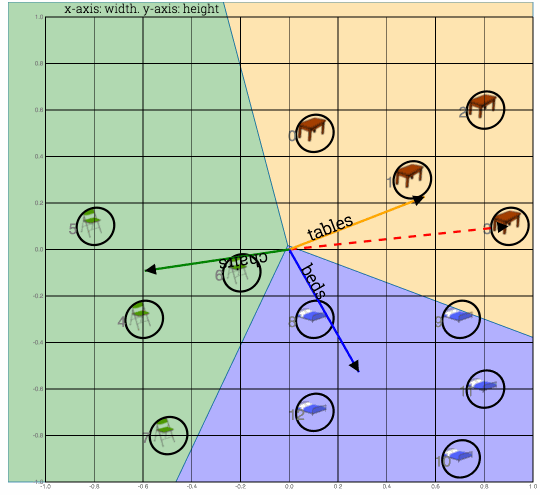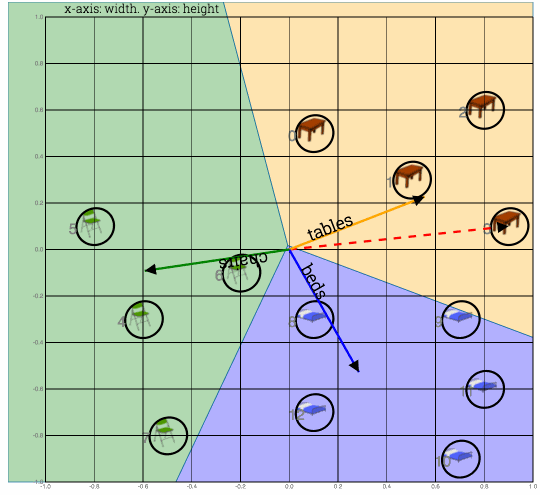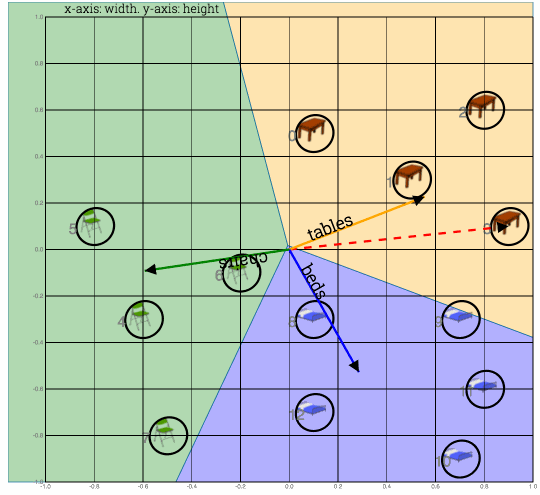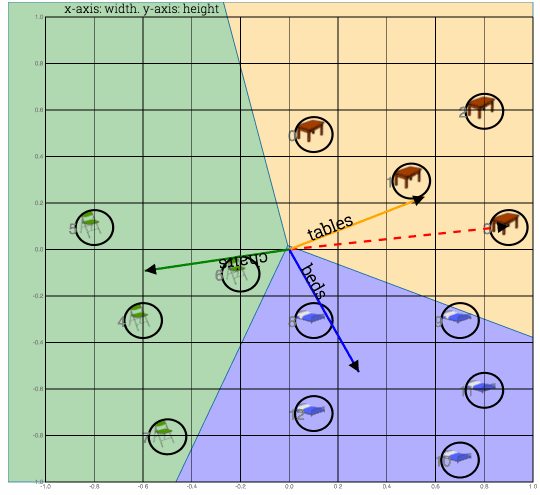
Data has to be ideally normalized so that larger values donot influence the classifier. In this case we used tanh(x) function. The restricted range could have been the range [0,1] if sigmoid function was used.

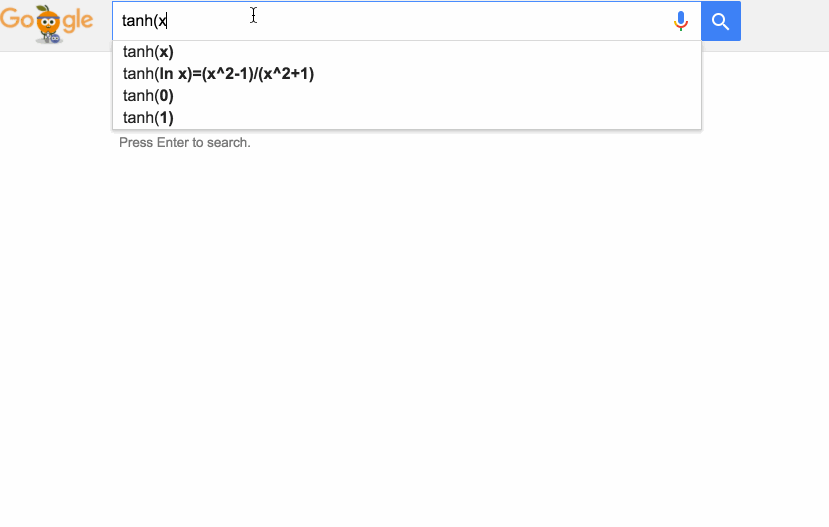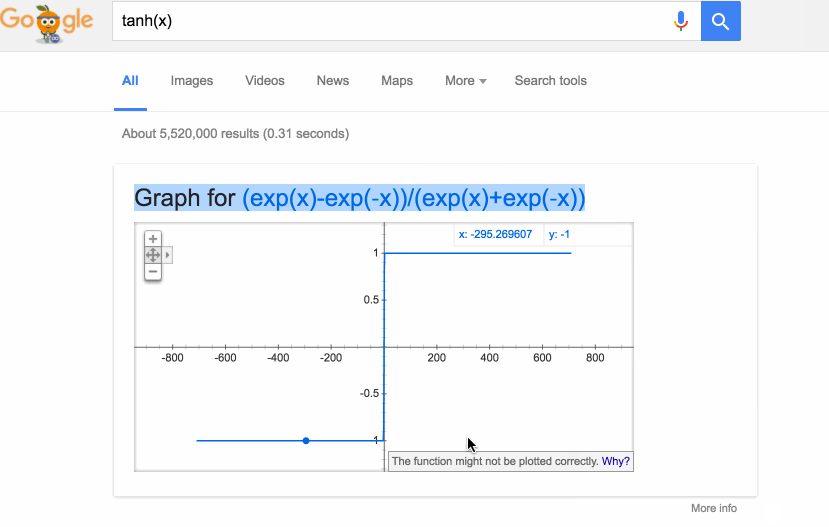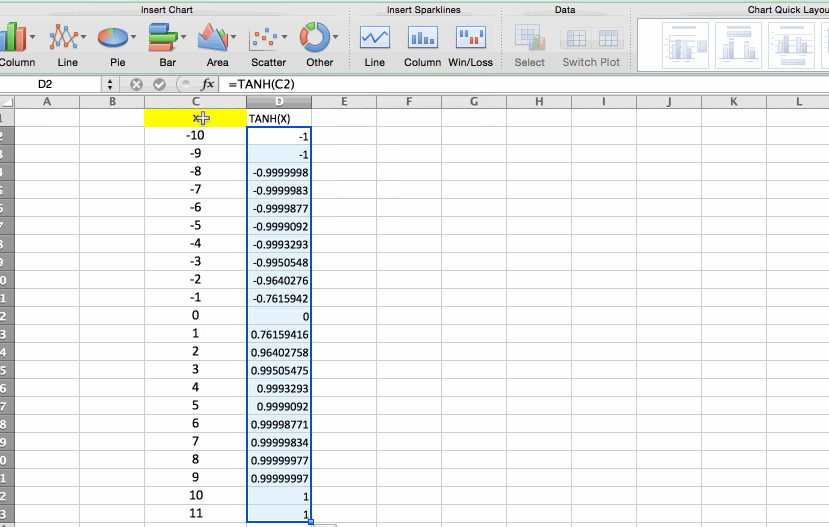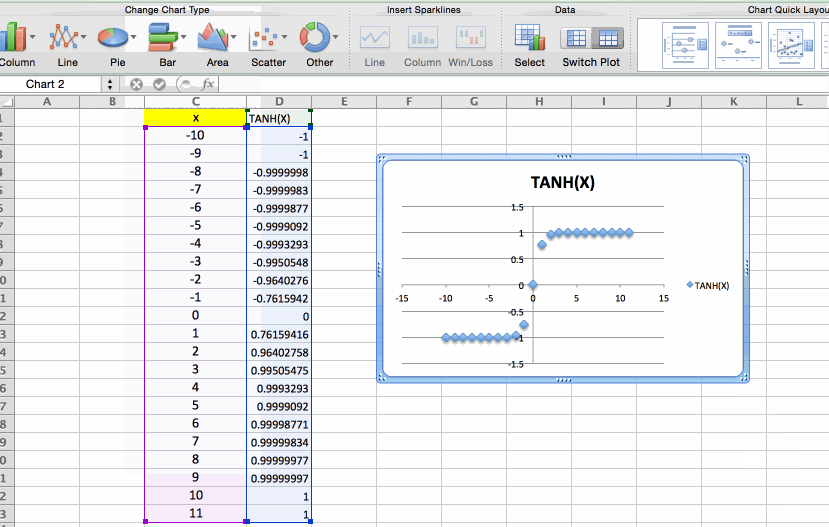
Fig: Demonstrating how tanh(x) function squeezes large values to a range [-1,1]

Stage1 of learning: Initialize weight vectors

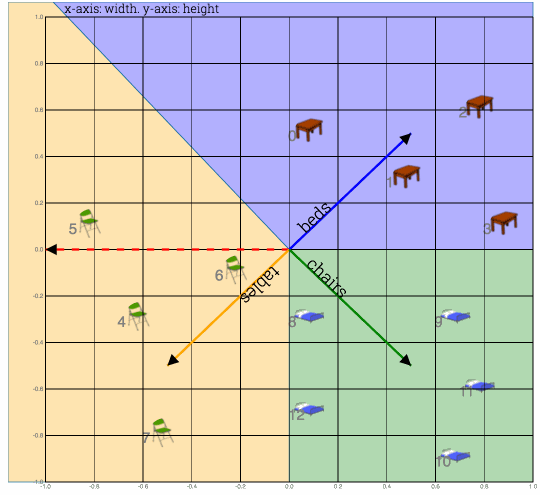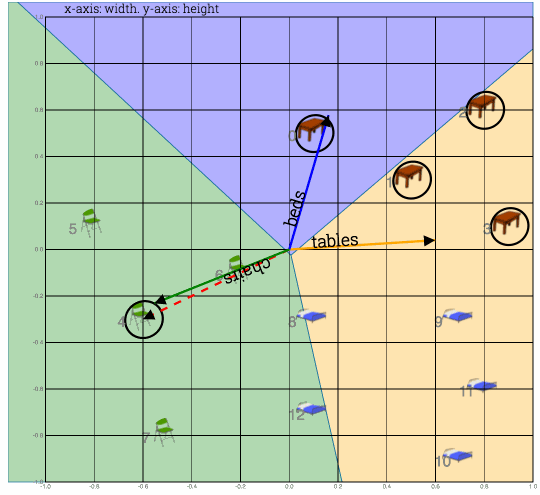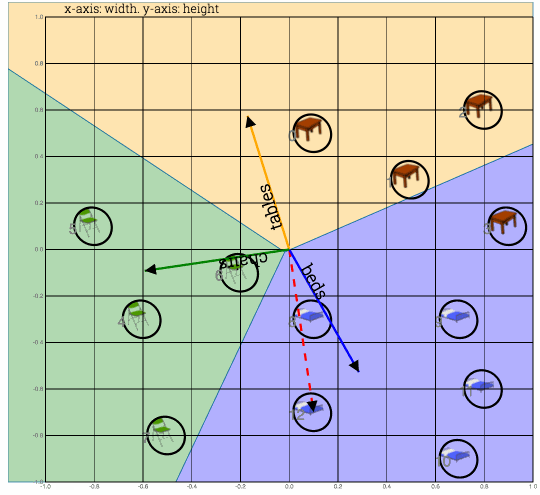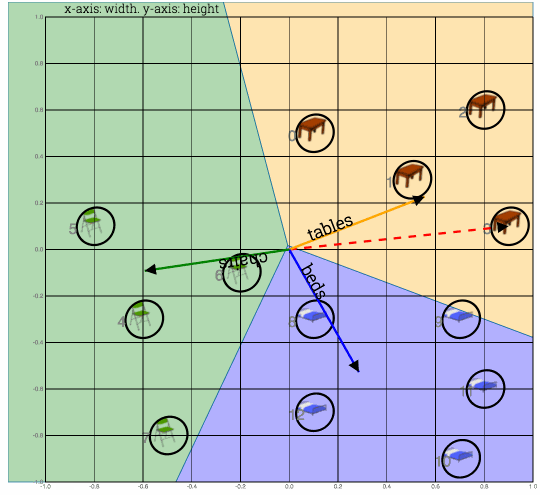
Weight vectors for each class of furtniture are initialized with random weights. Weights, also called parameters or coefficients are adjusted change to fit model to data. Which simple means that weights are changed to capture most meaning in data

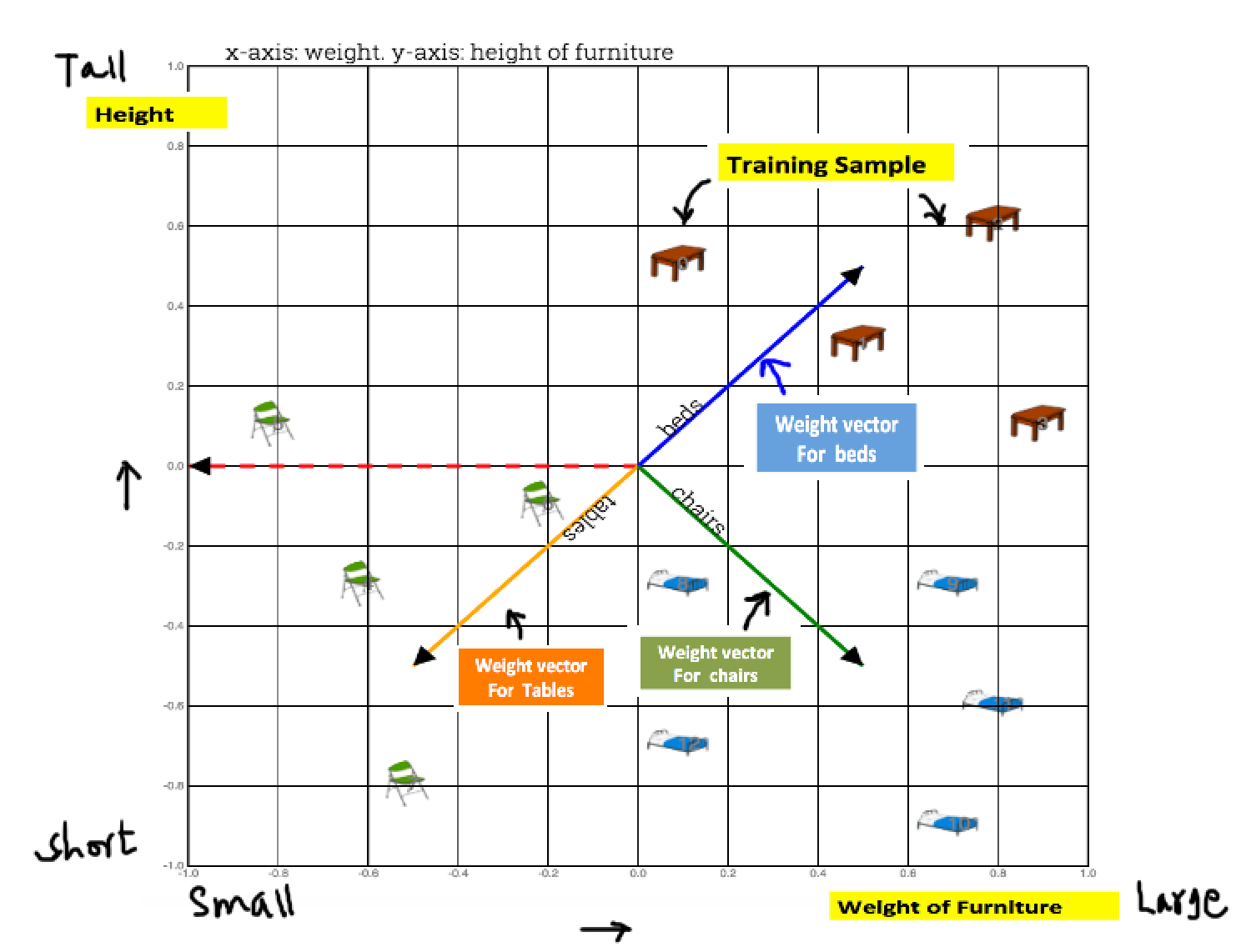
Fig1: Training samples. Height vs weight. To plot multidimensional data in 2-d refer to TSNE

Stage2. Implement Perceptron decision rule:

Walk through all training examples one at time.

Lets begin with table #0

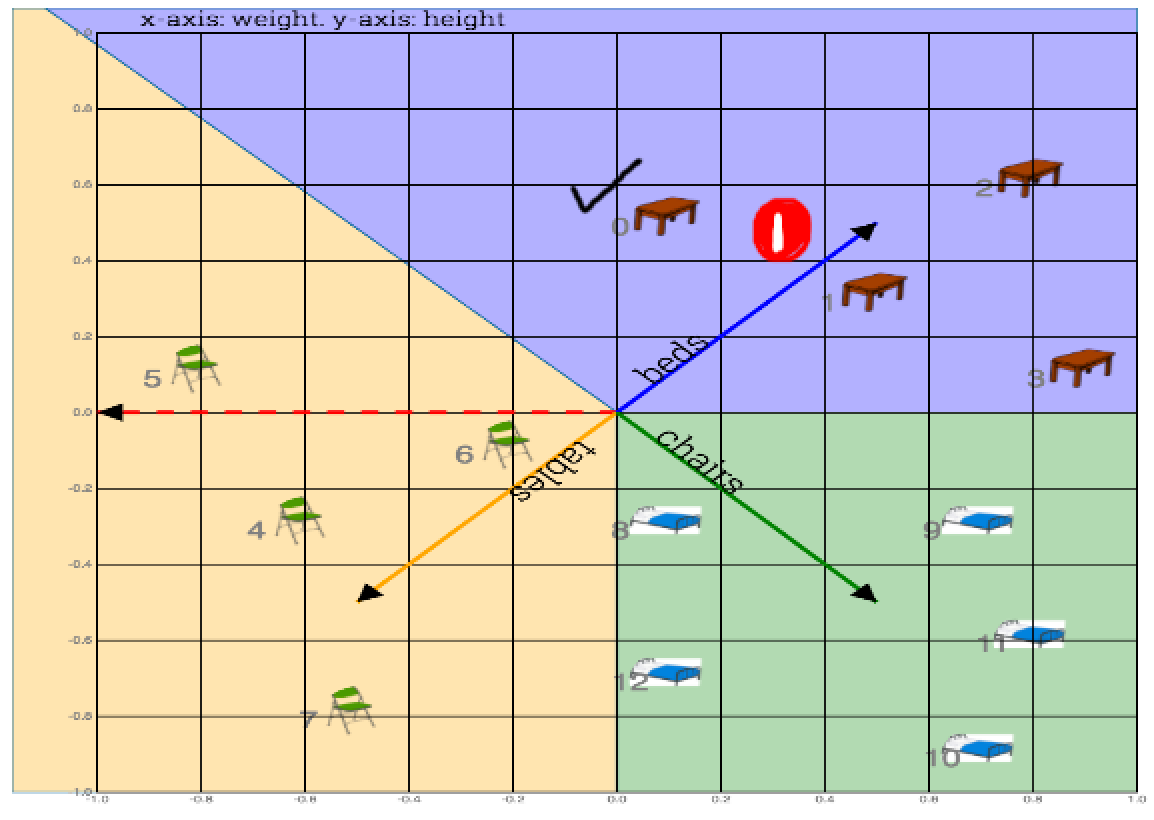
Fig: Weight vectors (one each for table, chair and beds) are randomly initialized. Goal is to align them towards correct cluster

1) Take dot product of table#0 with all weight vectors

2) Which ever weight vector has highest dot product wins. Label on that vector is your prediction

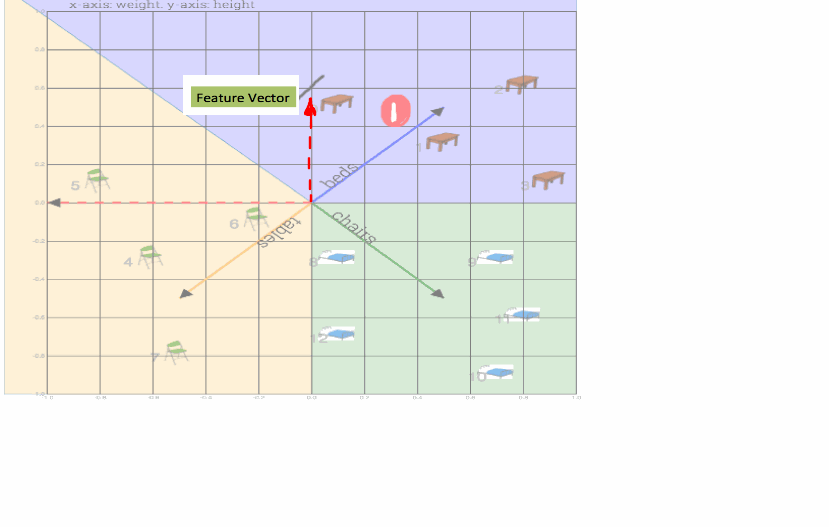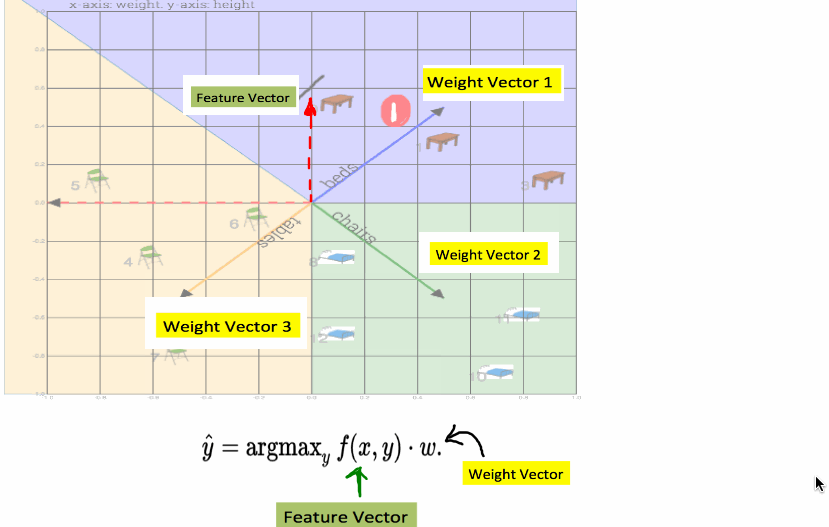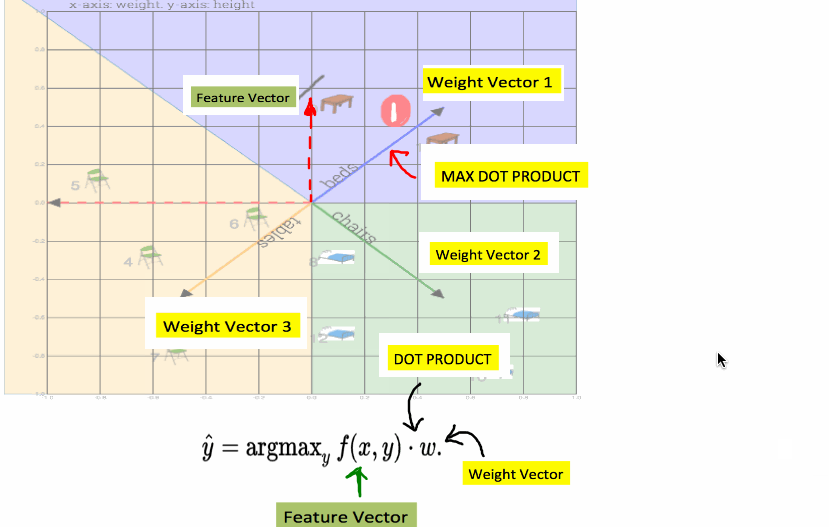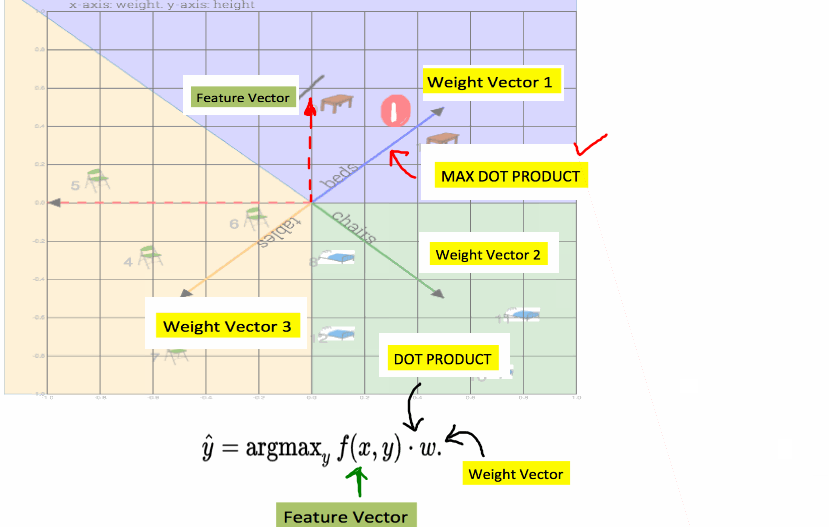
Fig: Shows calculation of dot product to compute a class (table or bed or chair). In this case closest weight vector was beds vector, while feature vector was a table vector. So prediction was wrong

2.a What to do when classfication is wrong

Move the weight vector, with max dot product, away from feature vector by subracting it from the curent training input.Bring the expected vector close by adding the expected vector to the current feature vector. This procedure is called delta rule.

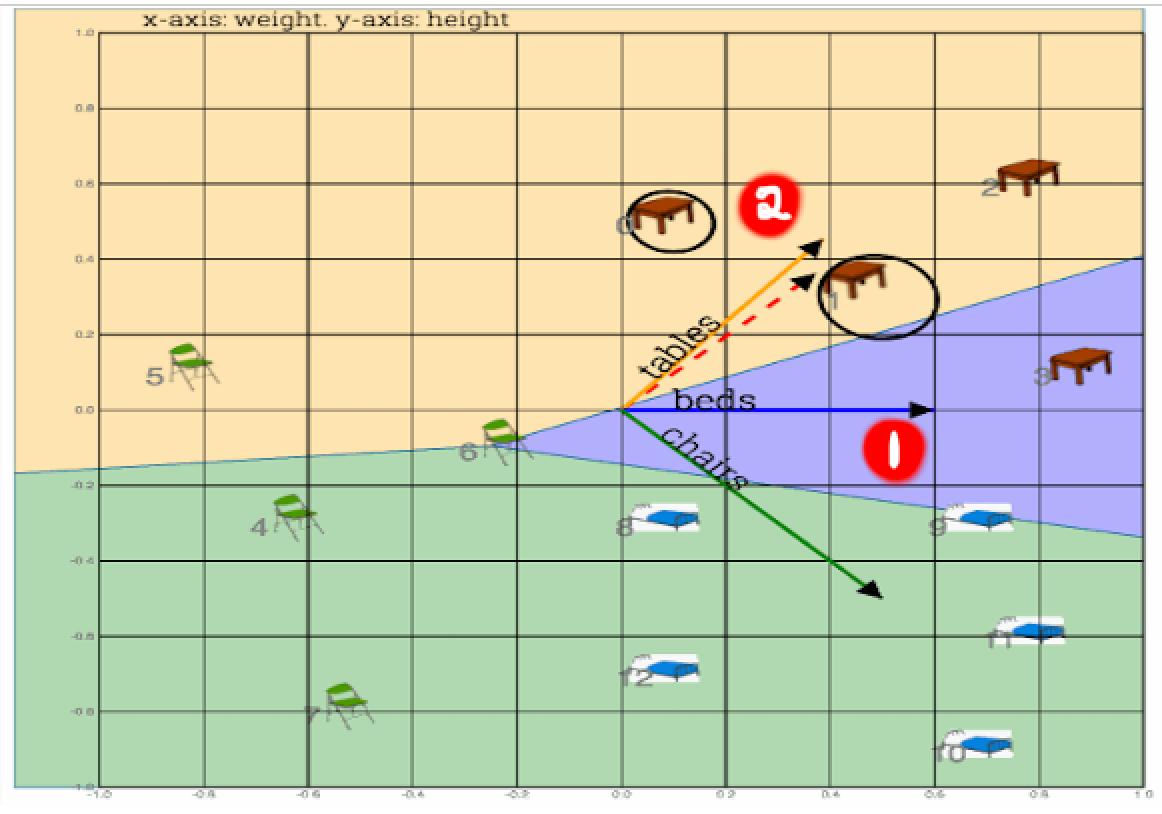
Fig: Here 1) Bed vector is moved away from table#0 and 2) Table vector is borught close to table#0

2.b What to do when classfication is right

Move the weight vector close to data point. Choose a lower learning rate to ensure that there are no huge jumps. Which could break convergence.

Notes

Learning rate matters. If learning rate is large, convergence takes longer

Weight vectors have to be normalized. That is their size has to be clipped to standard size

Conditions have to be set to stop learning after weights have converged.

Example perceptron

Section2: Problem/limitations with Perceptron

Problem#1: Noise

Perceptron Fails to converge with when data is not seperable. Weights might trash allover even when network seemed to have converged

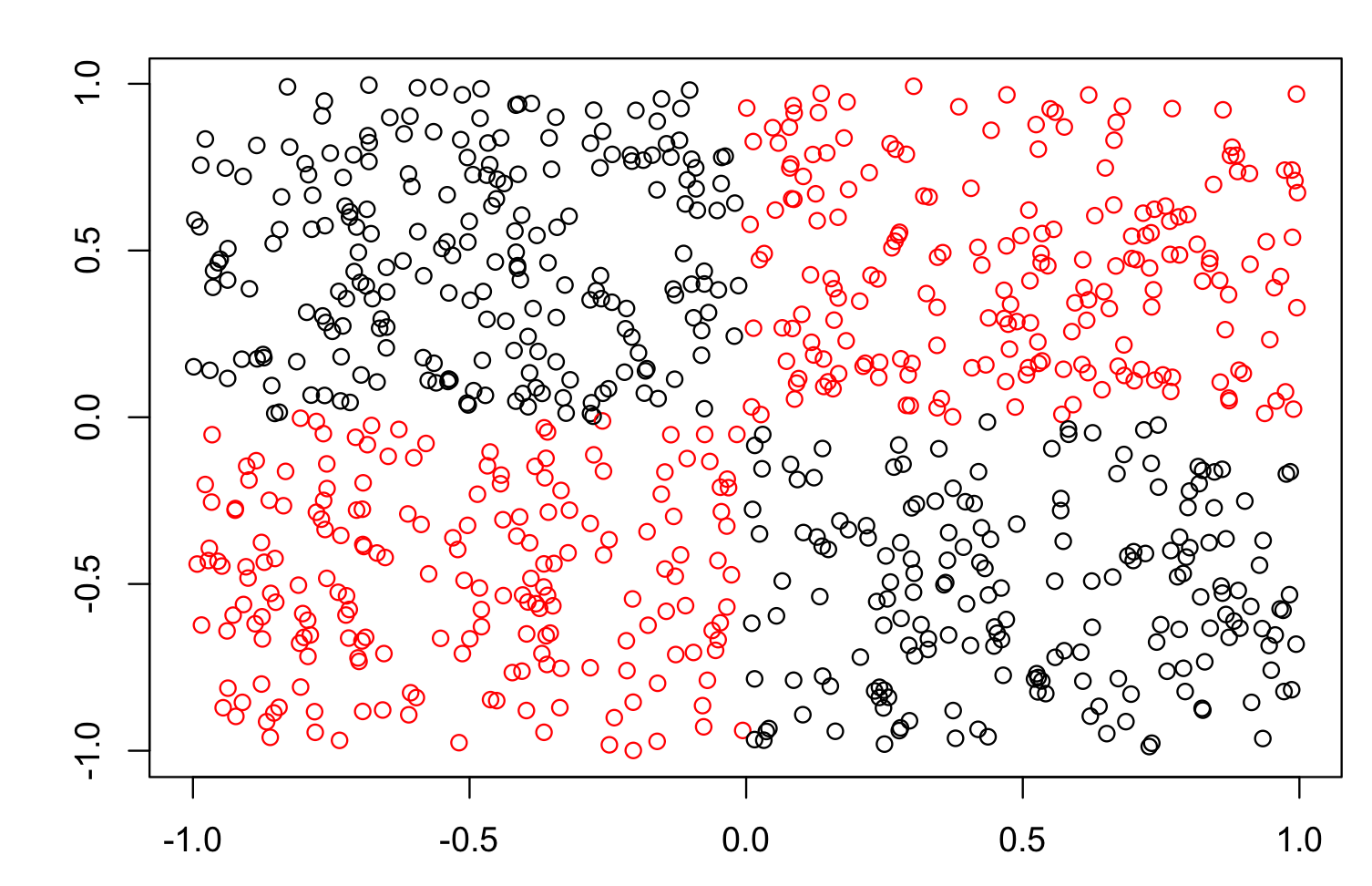
Fig: XOR data plot. Perceptrons donot converge with such feature vector pattern. Graph data is taken from mlbench package in R. Perceptrons work only with linearly seperable data.

Problem#2: Mediocre generalization

Perceptron doesn’t check to see is the chosen weight is most optimal.

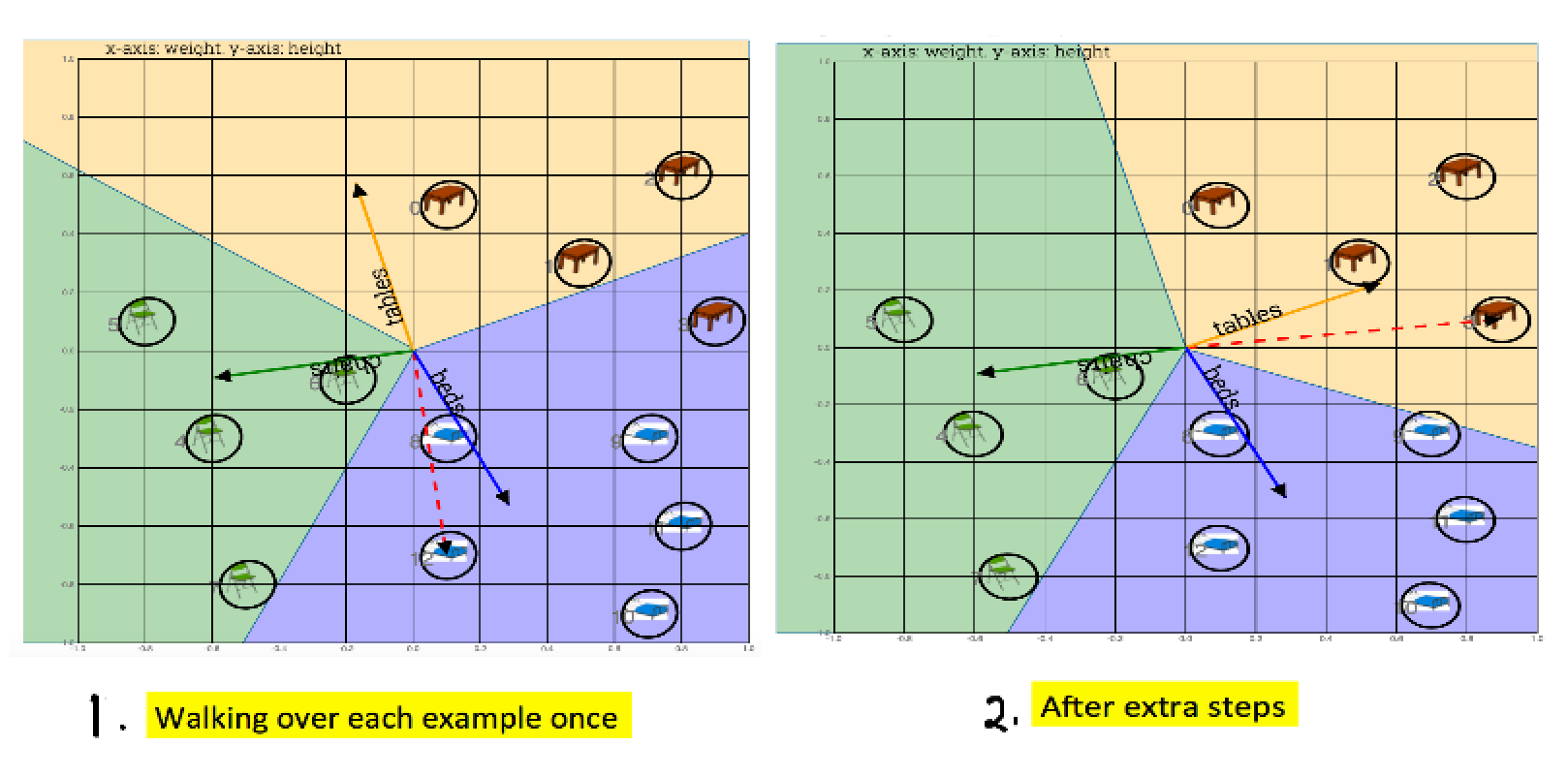
Fig: In this case, chosing additional walks through input training set improves the weights, but it doesn’t check if this would be most optimal.

Problem#3: Over training

With large training set, error rate is low, but with new test it doesn’t generalize, it just memorizes

How to overcome limitations:

Use hidden layers with Multi layer perceptrons to include interaction operator across variables

Implement a cost function to final optimal iteration to stop at reasonable convergence

Delta rule with backpropogation to adjust weights based on error feedback

Pocket Algorithm, Adatron optimization and Support vector machines Reference

Combine several of them together as is done in multi-layer networks

Seciton3: Lessons learnt:

Weight vectors could explode or diminish quickly. That is, weight vector could get too long after subsequent additions, or could beccome too small. To overcome that problelm, I normalized the weight vectors to a restricted length.

It is hard to figure out when to stop training. For this tutorial purposes, I hardcoded, number of iterations. It is highly probable that you might lose a converged state with small weight updates. Use a cost function to monitor accurate and inaccurate clasificatons to avoid over training.

You might like my other blog posts

In #MachineLearning, Cross Entropy is used to compare approximate models. Tutorial: https://t.co/cScdGGutXD #DataScience by @pavanmirla pic.twitter.com/mYuh2m6ov5

— Kirk Borne (@KirkDBorne) October 11, 2016

Build a Neural Net to solve the Exclusive-OR (XOR) problem: https://t.co/QmH0wzwOdA by @pavanmirla #DataScience #MachineLearning

— Kirk Borne (@KirkDBorne) September 16, 2016

Intuition behind concept of gradient vector: https://t.co/vejnoSADmr #DataScience #MachineLearning by @pavanmirla pic.twitter.com/DKcX1p9X4m

— Kirk Borne (@KirkDBorne) July 17, 2016

Maximum Likelihood Estimate (MLE) and Logistic Regression simplified: https://t.co/CUdOhpP4ko #DataScience #MachineLearning by @pavanmirla

— Kirk Borne (@KirkDBorne) July 25, 2016

Reference Interaction term