Tweet

Lets begin with a story. Dino, our little dinosour, is at location (10,5).Temperature @ (10,5) is 16 degrees celcius. Dino wants to move to colder place a soon as possible

Fig1:Screen capture from Good dino movie

Temperature distribution of the lake is

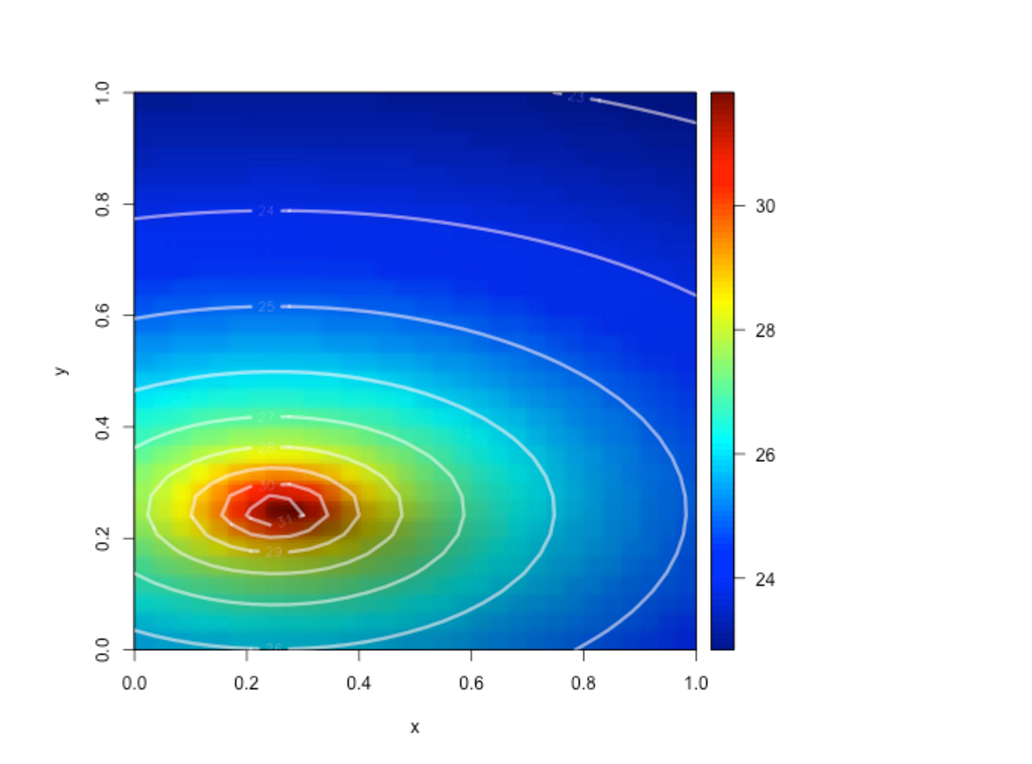
Fig2:Those concentric circles are called contours

Let me introduce you to technical terms - vector and gradient.

To explain vector, let’s look in to the picture below

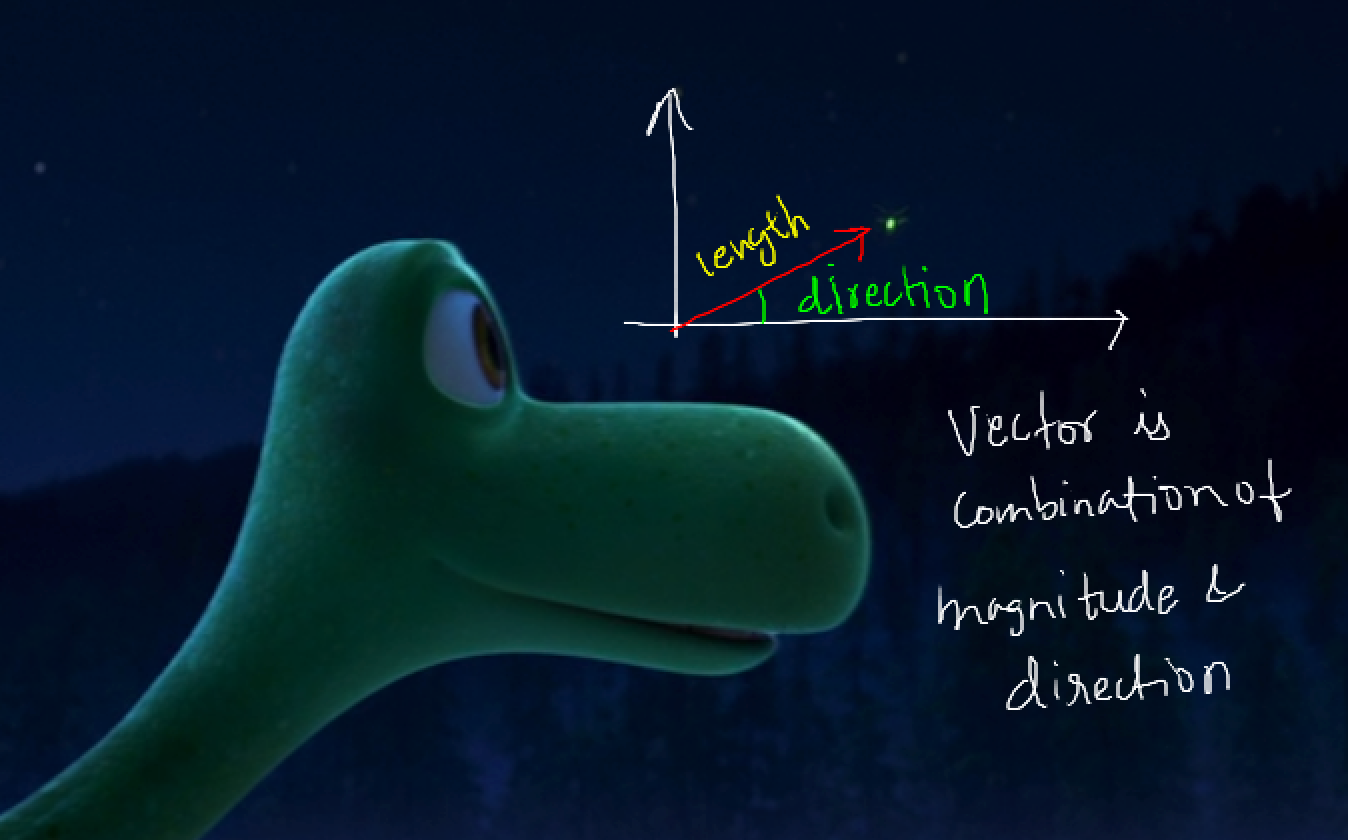
Fig4: Vectors are defined by a magnitude (the length of the vector) and a direction

Now lets define gradient. Gradient points in the direction of the greatest rate of increase of a function.

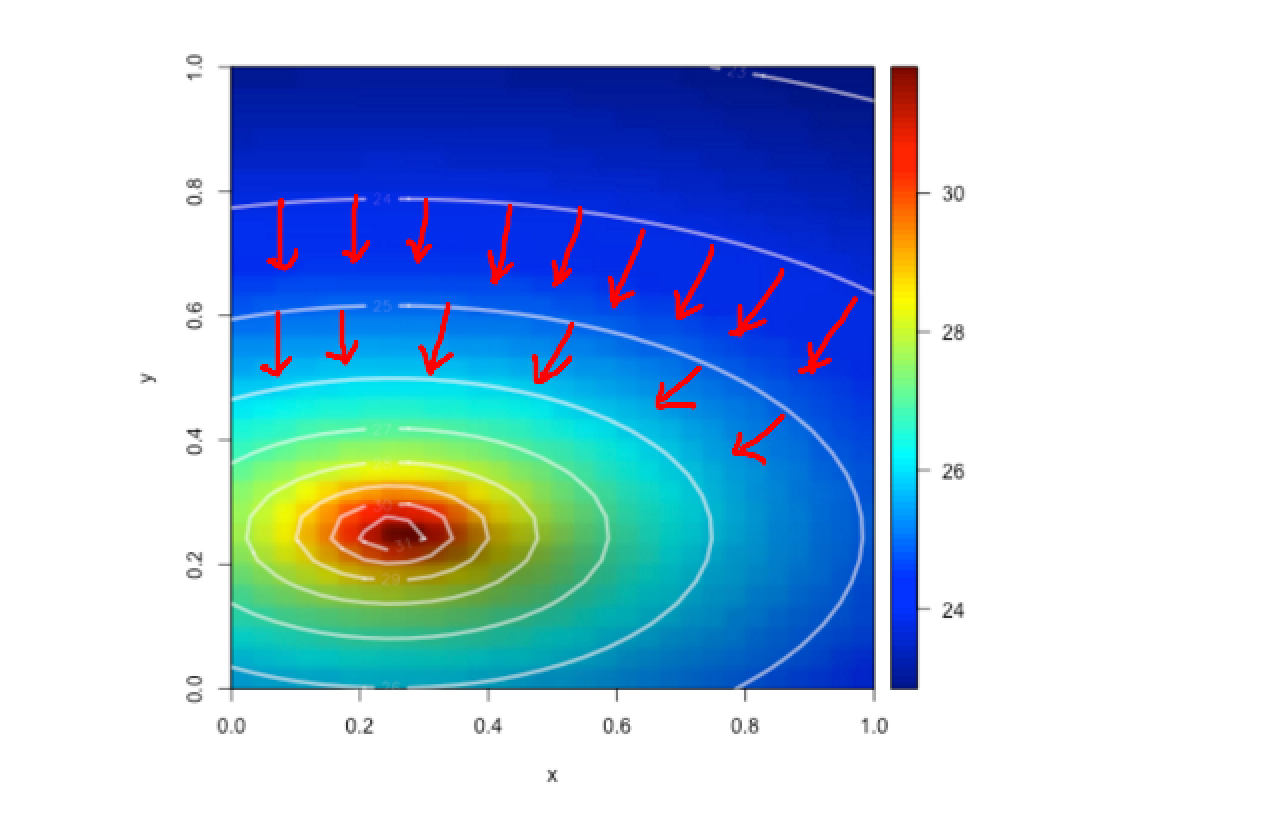
Fig4: Gradients ( at all points) are vectors pointing towards greater increase in temperature

To get the direction of the greatest rate of decrease of Temperature, take negative of gradients at each point

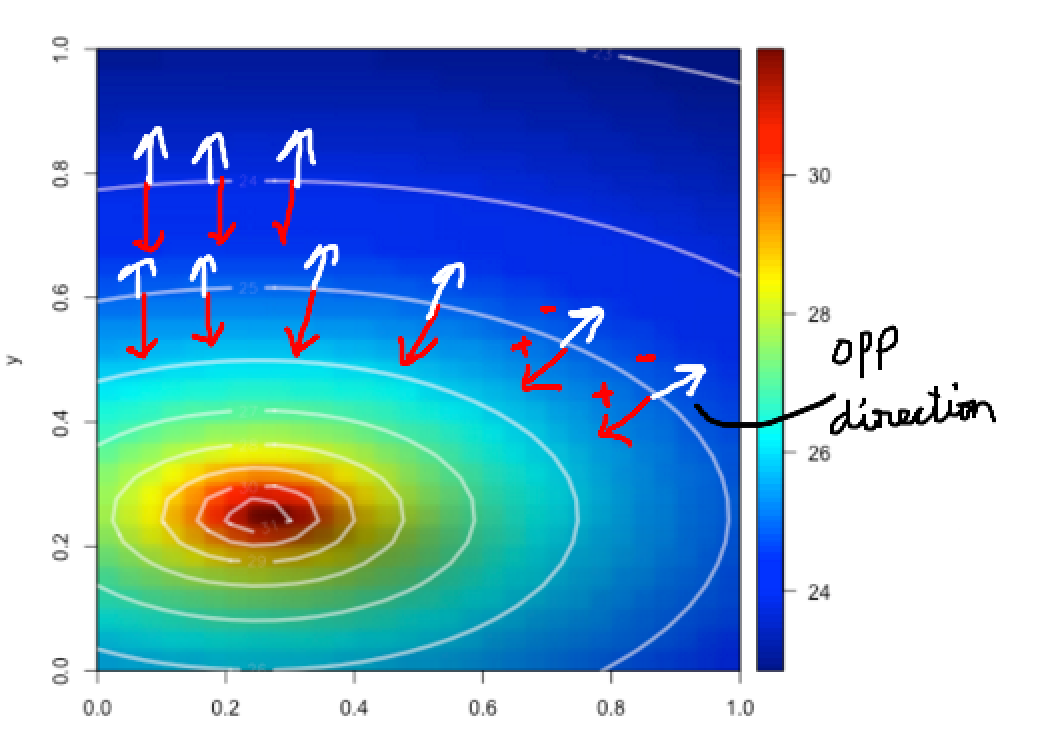
Fig5: Negative of gradients are pointing towards greater decrease in temperature

To move to a colder location, Dino should swim in the direction of greatest decrease in Temperature.

Let us use some basic linear algebra to find the gradient vector at point (10,5)

Find partial derivatives with respect to x and y directions

​

Remember we will take negative of gradient

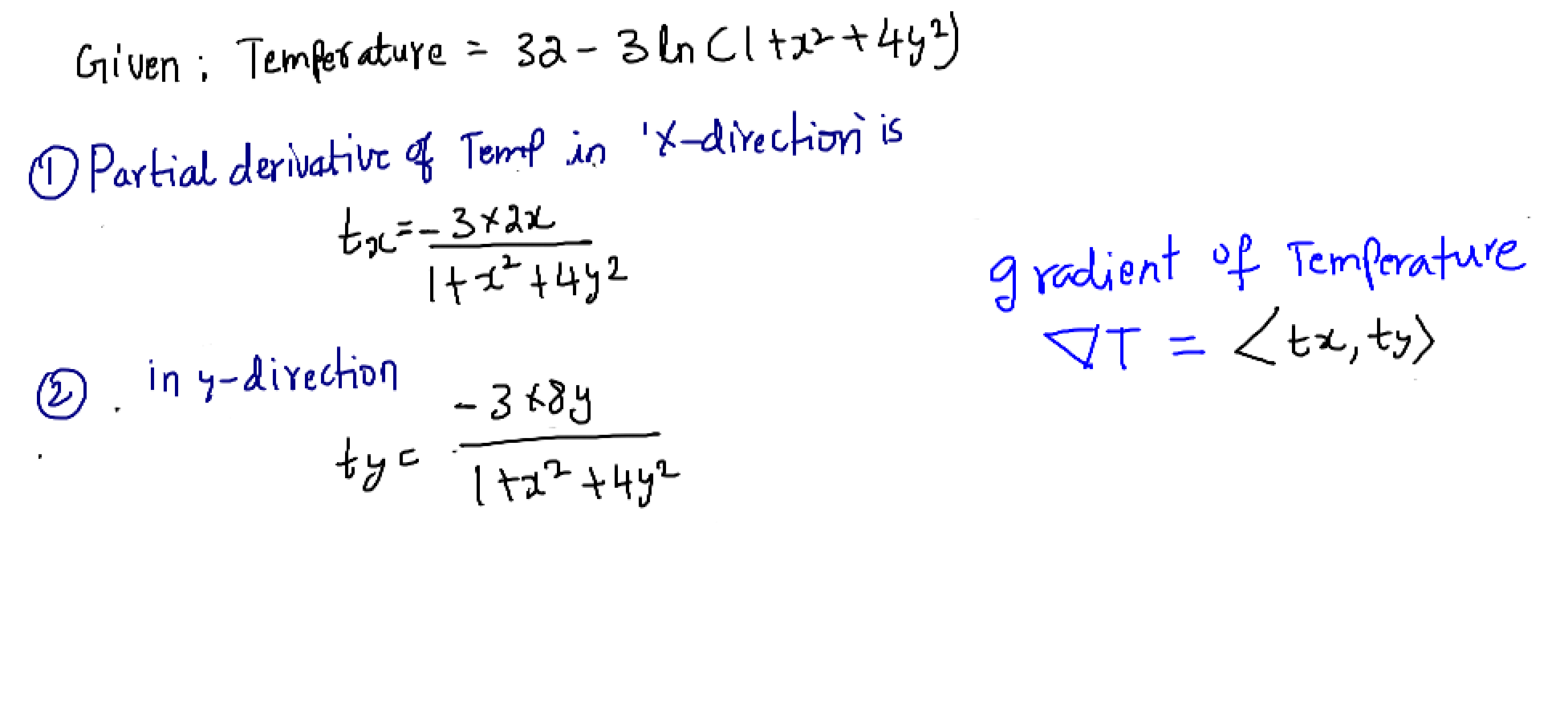
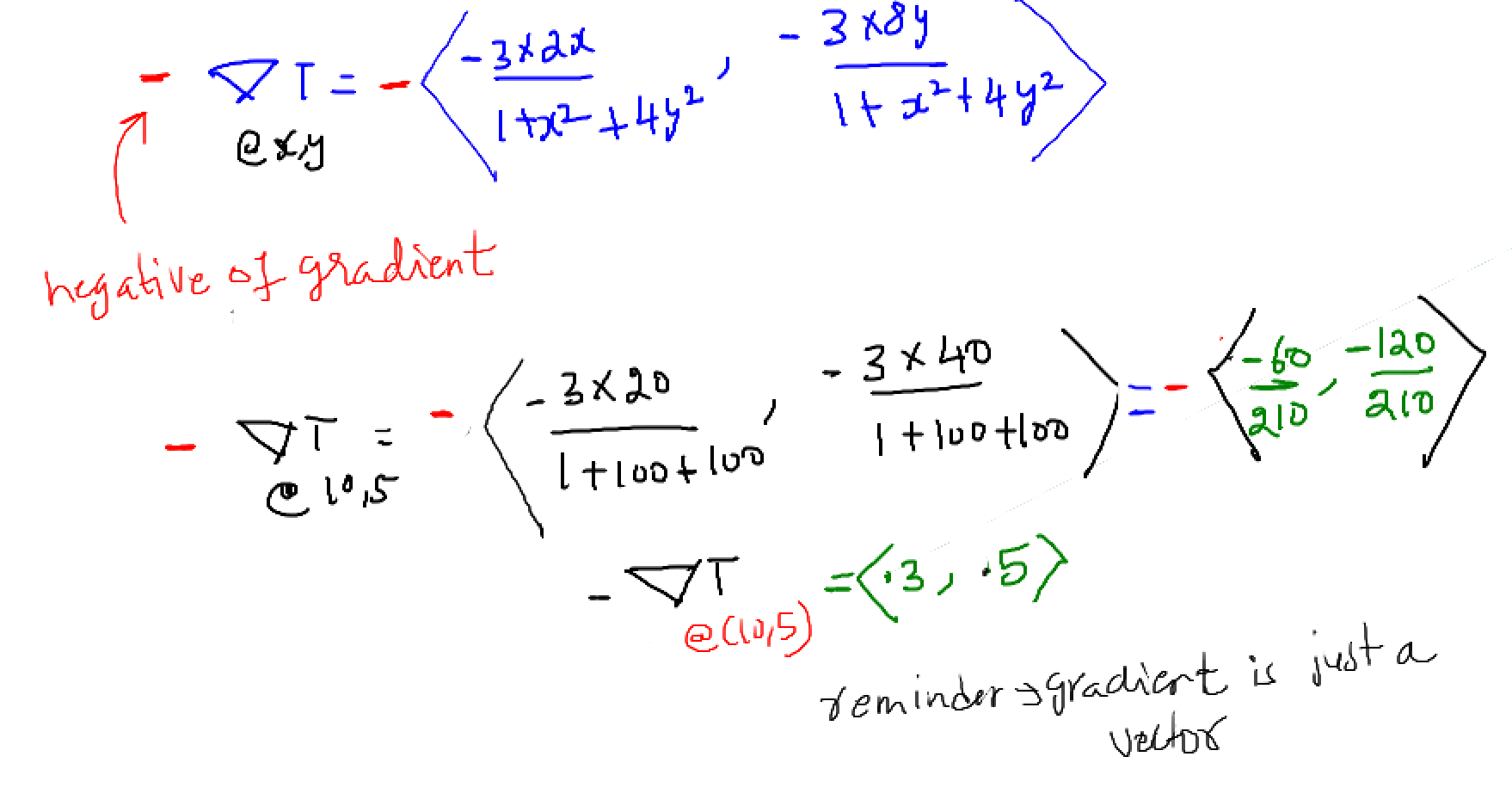
Fig5: Gradient vector suggests that dino should move to the (right and then up) from current location (10,5)

Fig6:It is importanmt to note that this direction is clearly not directly towards the coldest point, but rather is the direction of greatest decrease in temperature at the point.

Checkout these Directional Derivative Examplesinteractives

Tweet

Where is gradient vectors concept used?

Given, information about a function, you can find direction of greatest change in function. In deep learning, gradients are used to adjust weights and find direction of greatest change in loss function In finance, economics gradient concept can be employed to find direction of greatest change in function