Signature

Maximum Likelihood Estimate and Logistic Regression simplified

Jul 20, 2016

Video added: Feb 2018:

Quick introduction to Maximum Likelihood Estimation

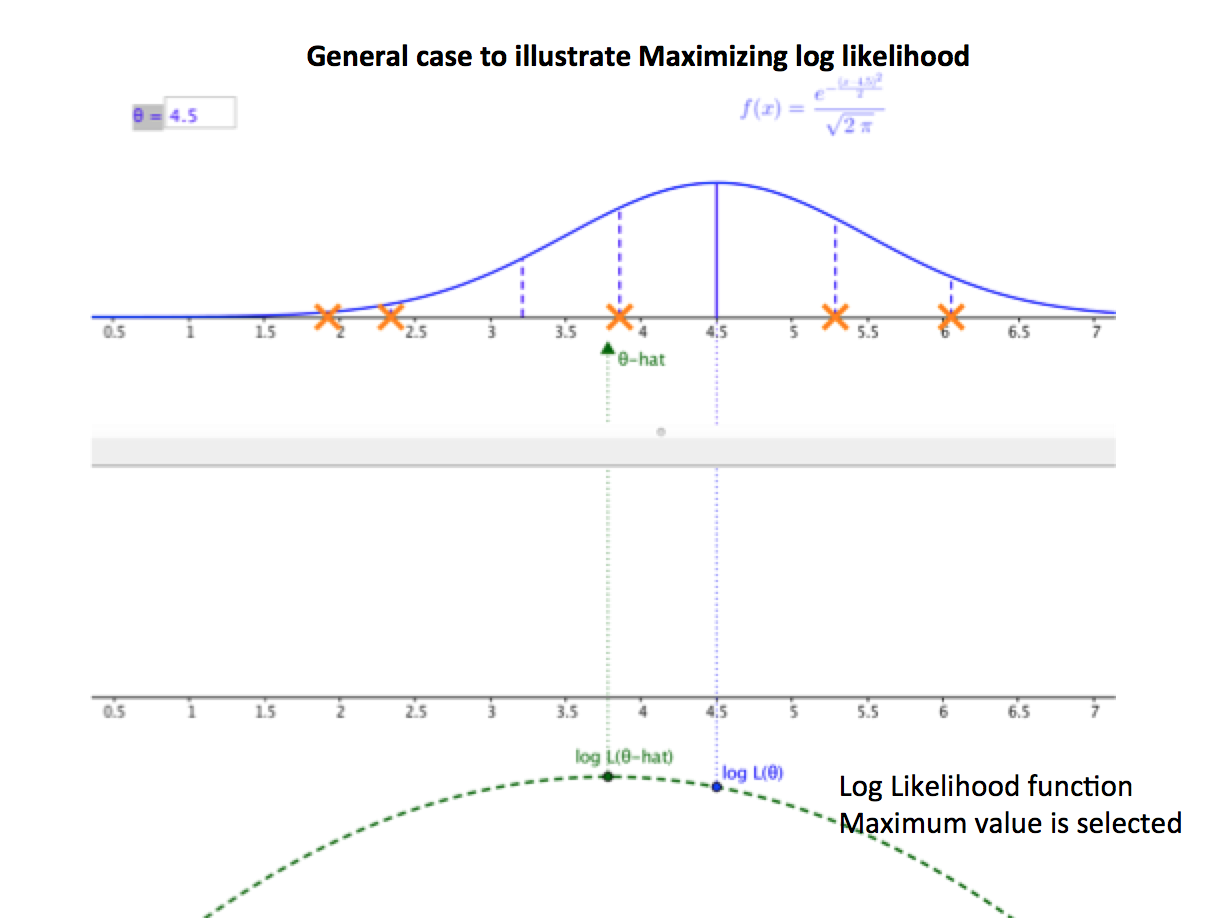
MLE focuses on the fact that different populations generate different samples. The figure below ilustrates a general case in which the sample is known to be drawn from a normal population with given variance but unknown mean.

Assume that observations came from either distribution A or distribution B.If the true population were A, the probability that we would have obtained the sample shown would be quite large.

Next -> Likelihood function

Logistic Regression example

Our Bank Manager wants to build a prediction model to predict if a customer will payback the loan

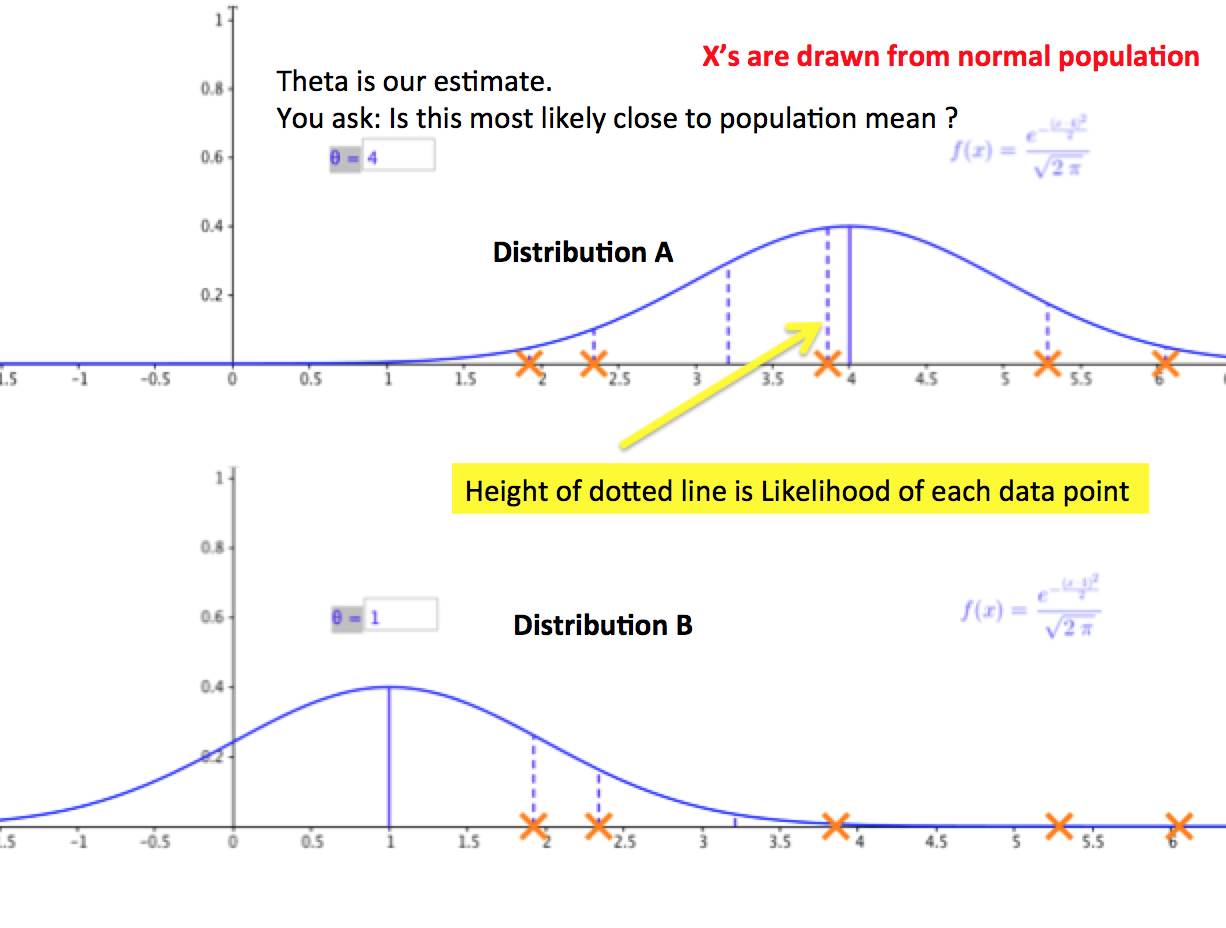
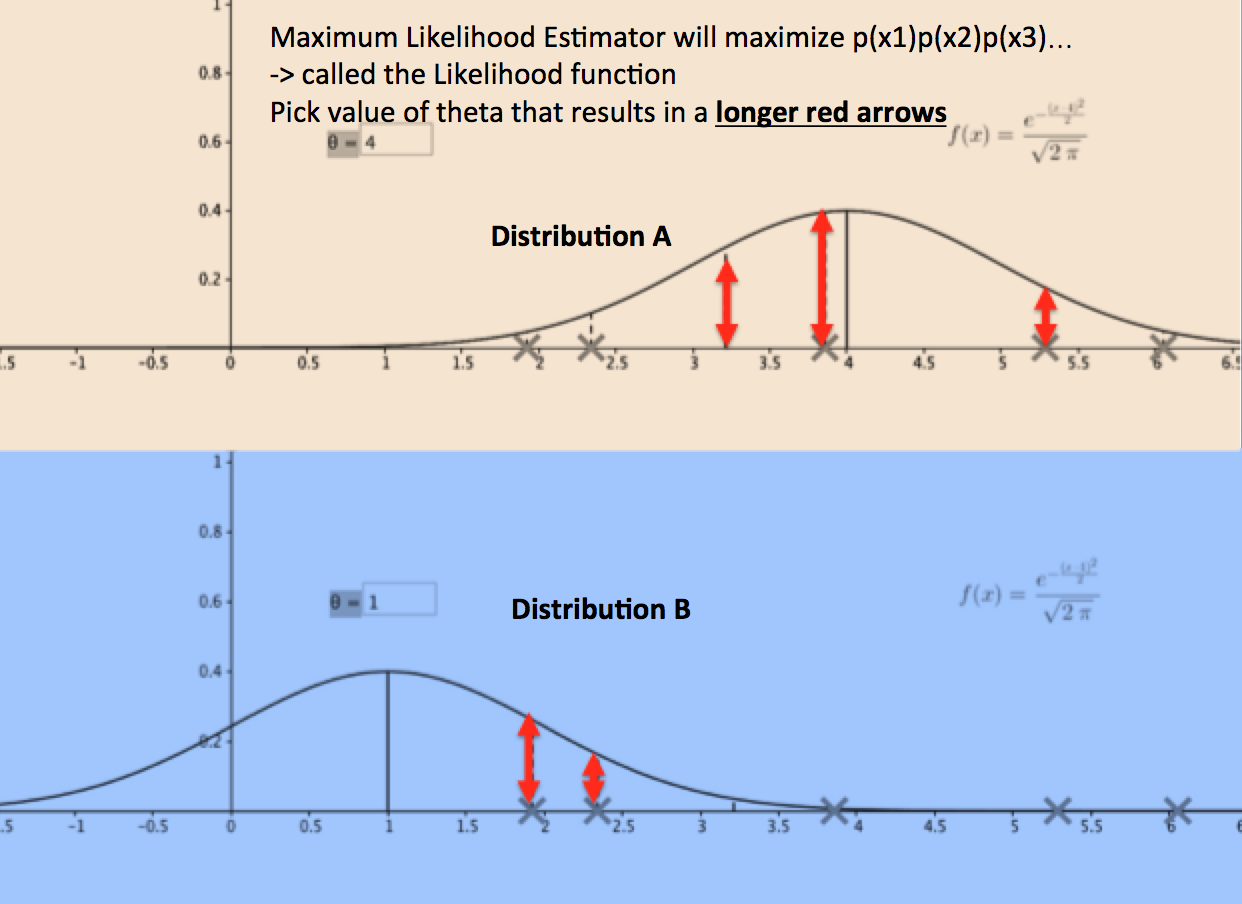
Fig1: clip from movie zootopia

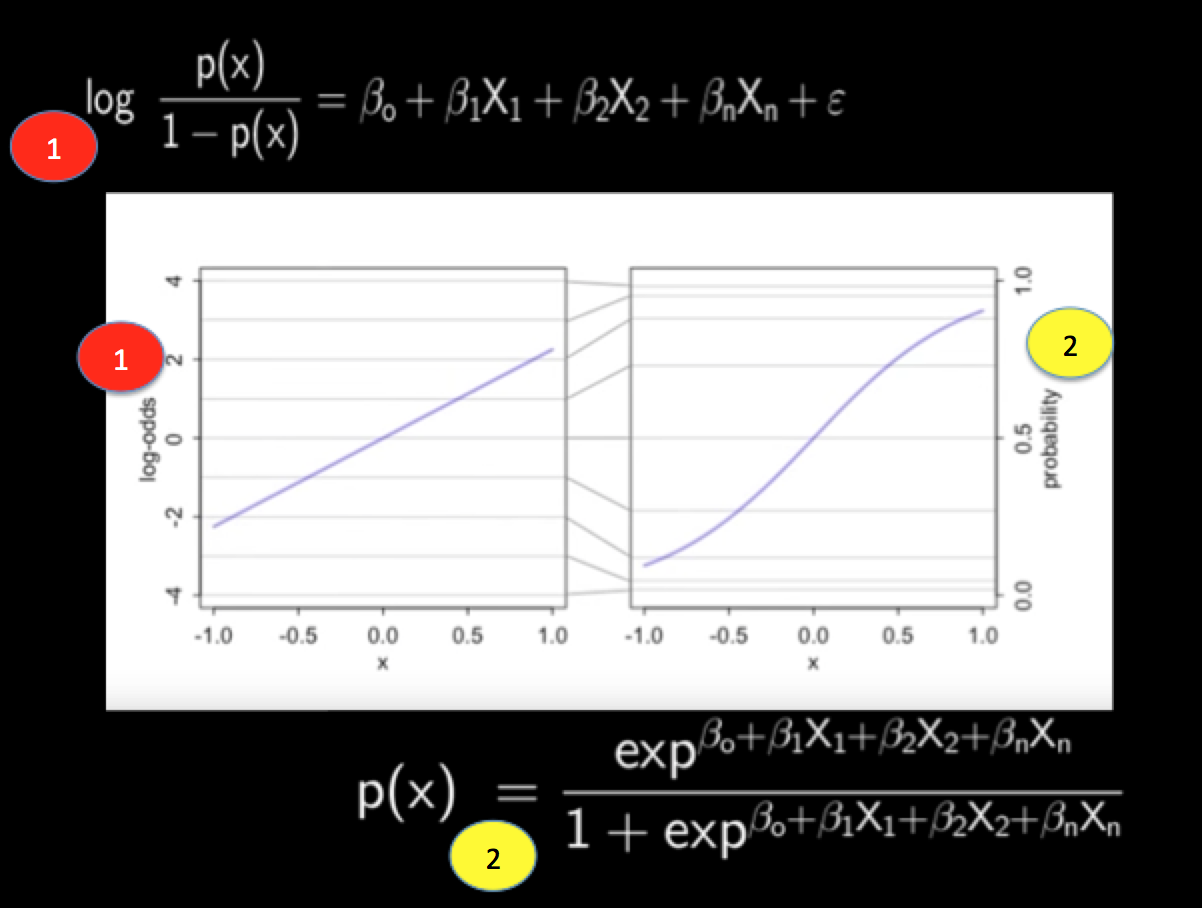
A statistician advised our Bank Manager to use Logistic regression

Why not use linear regression?

Least squares regression can cause impossible estimates such as probabilities that are less than zero and greater than 1.So, when the predicted value is measured as a probability, use Logistic Regression

Let’s begin with understanding elements in our model

Download spreadsheet here Conrad Carlberg’s book- Decision Analytics: Excel

Known data and parameters are highlighted. Note that coefficients will be adjusted with Solver in next phase

In the image below, Logit, Odds, Likelihood,Log Likelihood will be claculated based on estimated coefficients that try to maximize objective function

  • 1

    Logit: Setup logistic regression equation

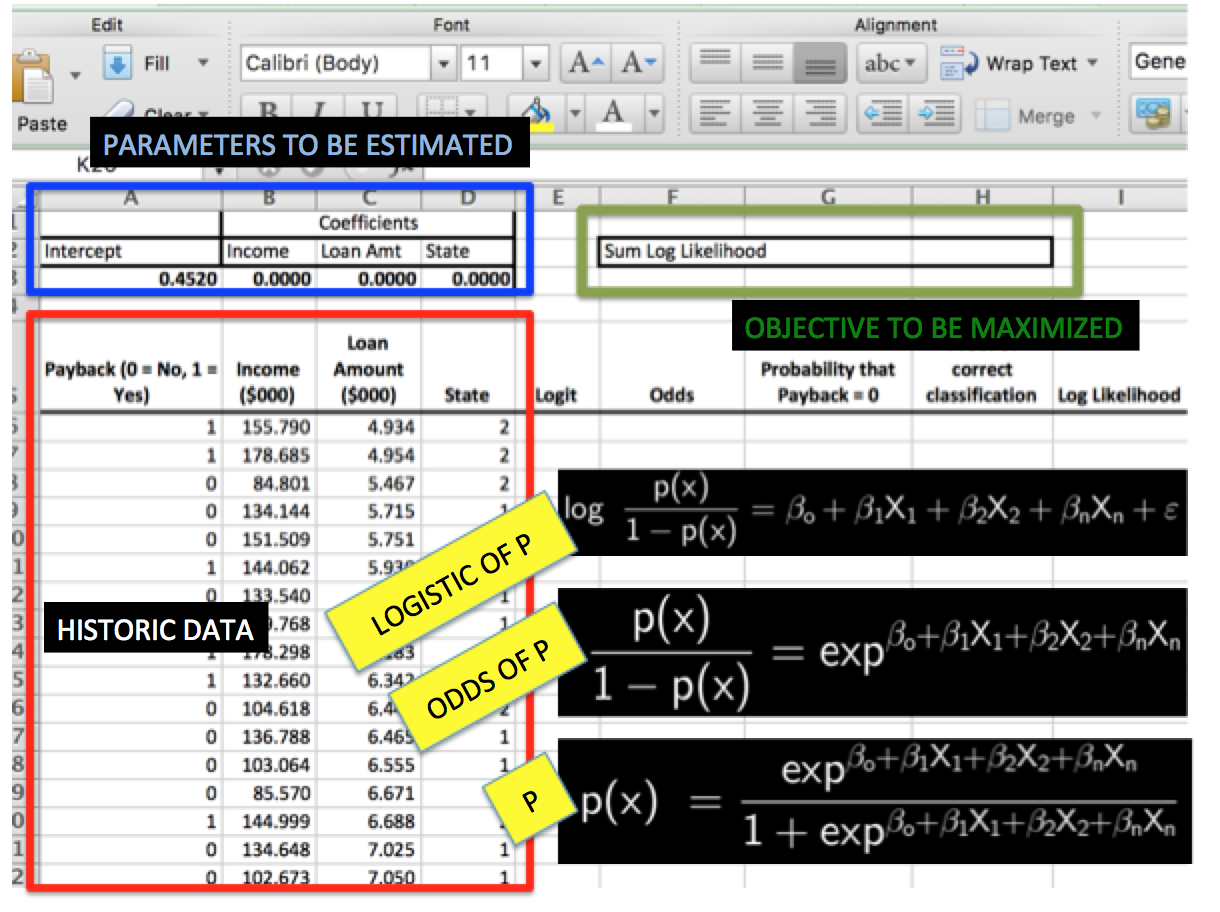
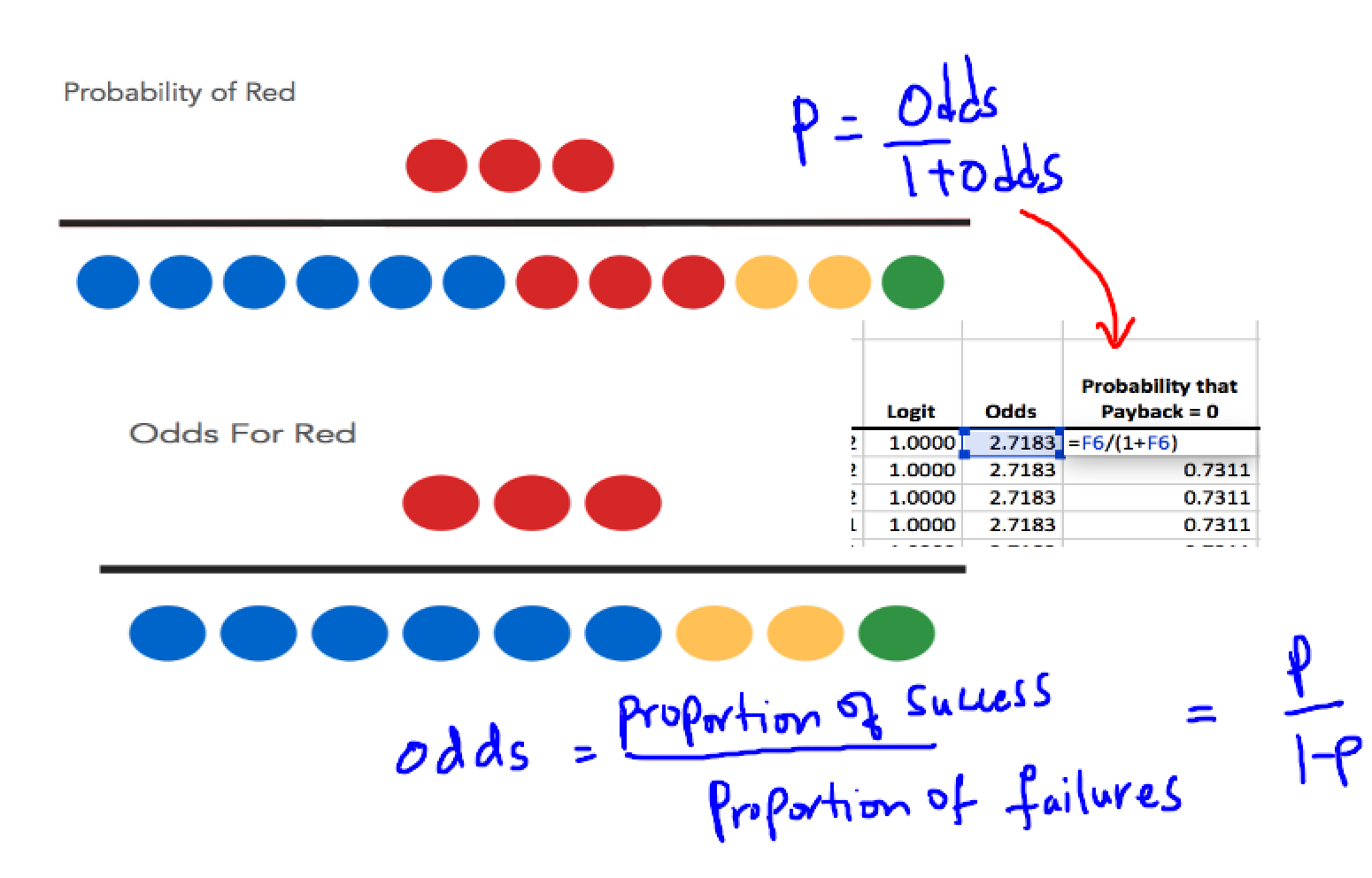
    We use the log of the odds rather than the odds directly because an odds ratio cannot be a negative number—but its log can be negative.

    Logit formula

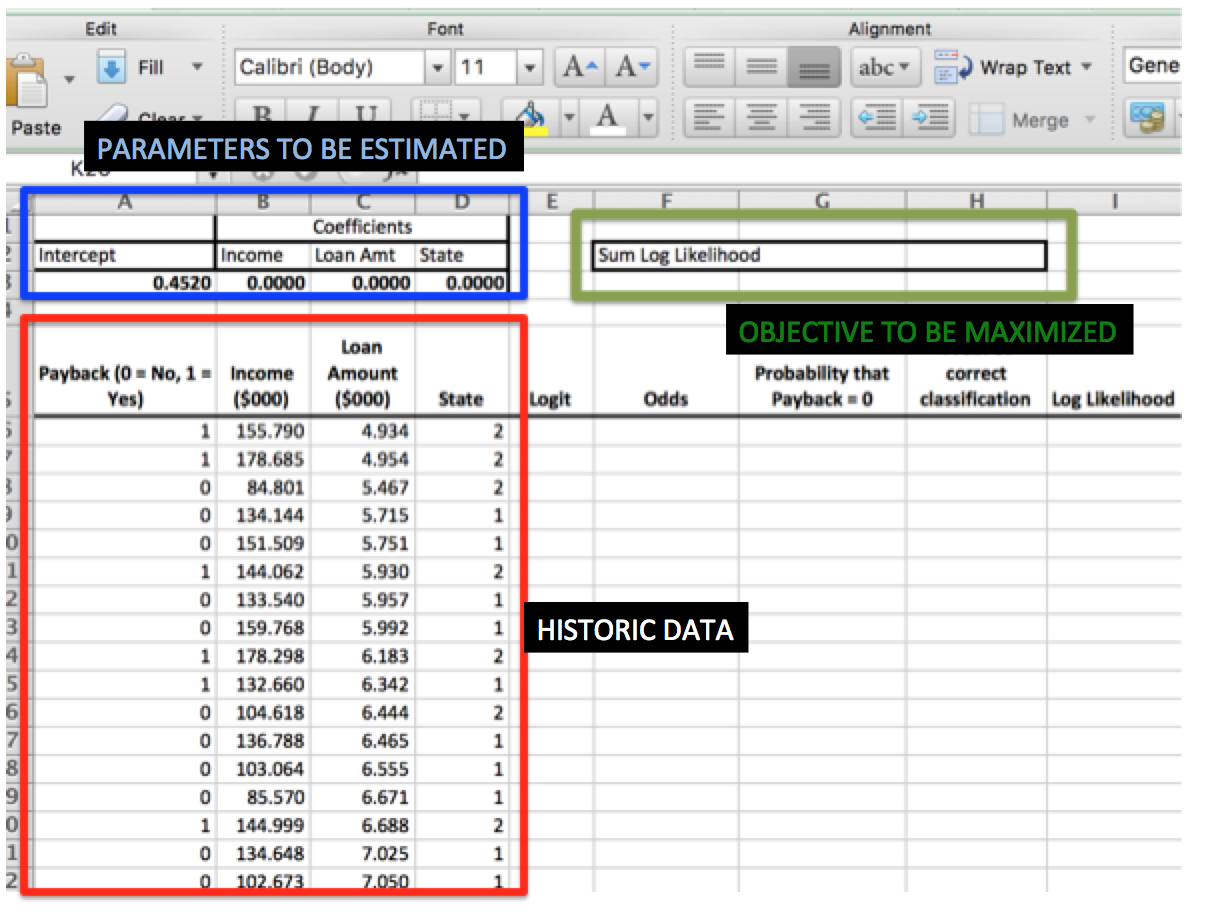
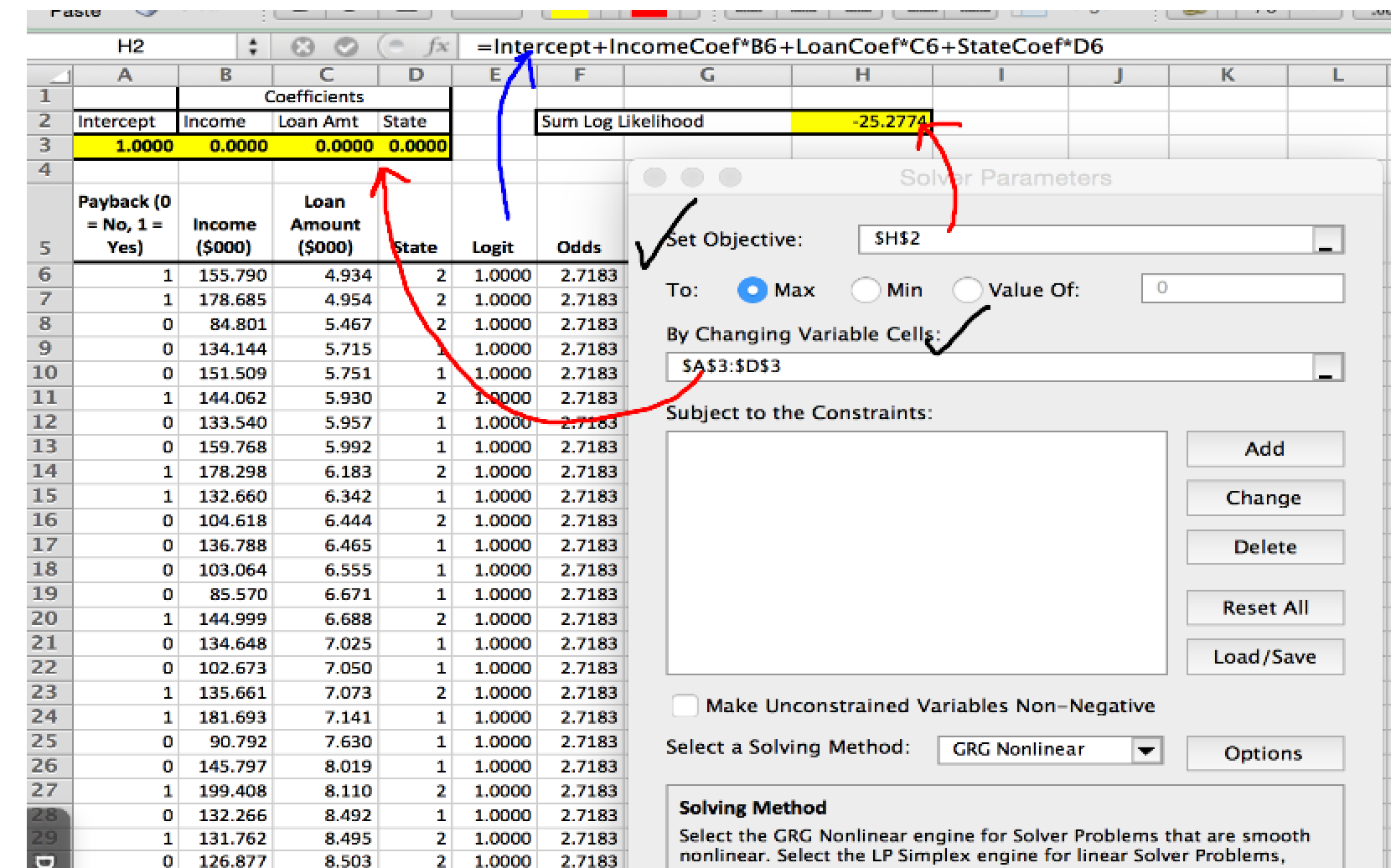
    Notice that we have randomly initialized our coefficients for income and other predictors. These will be adjusted by Solver based on a likelihood function.We will cover them later

    This video explains log-odds

  • 2

    Odds - Reflect the likelihood that the event will take place

    source titatnic example

    Here is how logit, odds and probability are linked

  • 3

    Probability that payback =0

    This column contains the calculated probabilities that each borrower will not repay a loan of a given Amount, given that the borrower has a given Income and other predictors

  • 4

    Probability for correct classification

    Column H tells us the predicted probability of the borrower’s actual behavior, whether that behavior is repayment or default—not simply, as in Column G, the predicted probability of defaulting on the loan. Outputs the probability of the datapoint’s belonging to a certain class

  • 5

    Log Likelihood

    It is possible in theory to assess the overall accuracy of your logistic regression equation by getting the continued product of all the individual probabilities

    Why natural log?

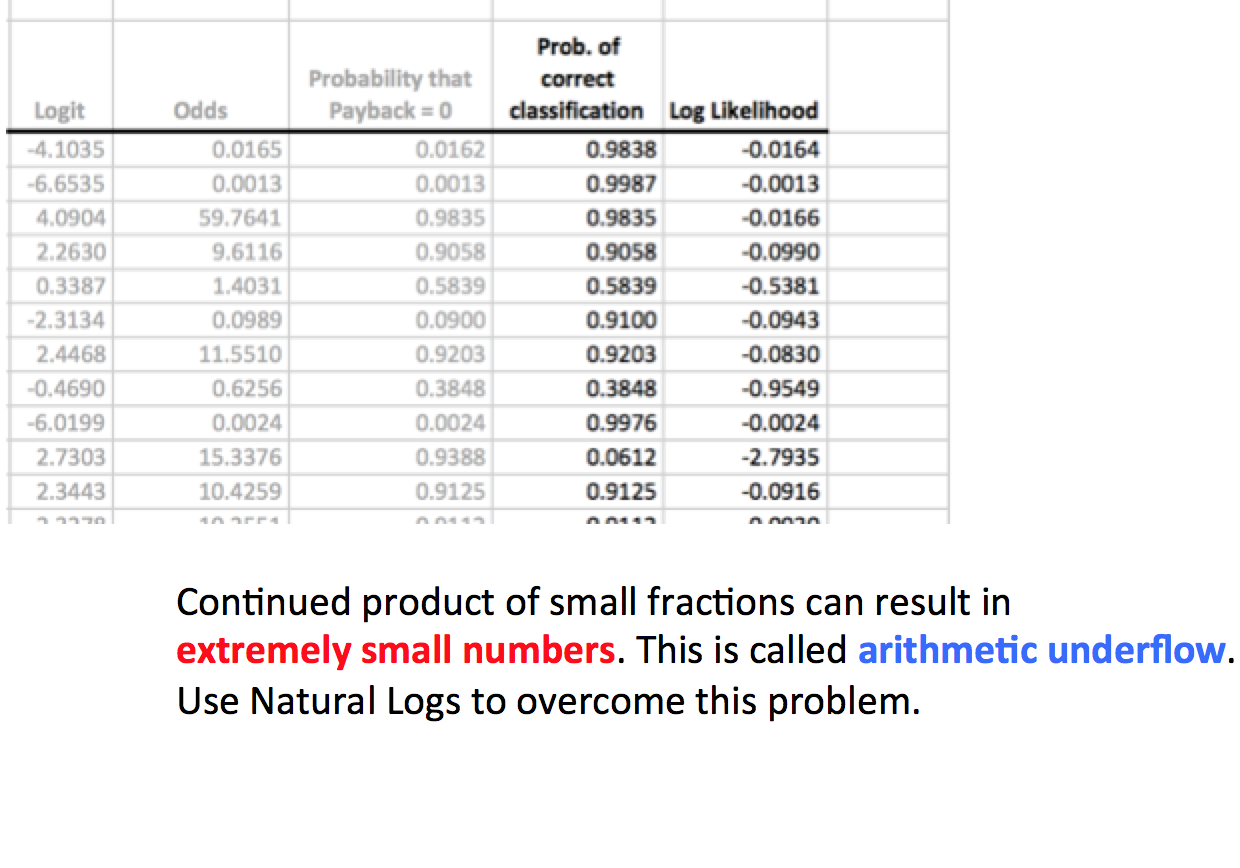
    One property of logarithms is that their sum equals the logarithm of the product of the numbers on which they’re based

Finally, Objective function

The logarithms of probabilities are always negative numbers, but the closer a probability is to 1.0, the closer its logarithm is to 0.0. Hence the Solver should be setup to adjust coefficients such that likelihood sum is maximum

Solver Instructions

Adjust the intercept and coefficients in such a way as to maximize the value in cell H2

How to interpret these calculated coefficients ?

Summary

  • 1

    Initialize coefficients for predictors

  • 2

    Setup regression equation and calculate log odds (Logit)

  • 3

    Calculate Odds and probabilities for every observation

  • 4

    Take log of likelihood to avoid arithmetic underflow

  • 5

    Setup Solver to maximize Sum of Log Likehood

I haven’t covered cross-validation, which is commonly used to validate a logistic regression equation.If you don’t always have a large number of cases to work with, a different approach is to use statistical inference. Will cover it in another blog post

comments powered by Disqus

Machine Learning Posts

Precision, Recall and F1 Score Secretary Problem. Strategy to select the Best Candidate A walk through Machine Learning Conference held at Toronto Introduction to the concept of Cross Entropy and its application Build a Neural Net to solve Exclusive OR (XOR) problem AI Winter. How Canadians contributed to end it? Perceptron Learning Algorithm in plain words Maximum Likelihood Estimate and Logistic Regression simplified Deep Learning highlights Month by Month Intuition behind concept of Gradient

Finance Posts

IPO Stocks Performance in 2019 S&P500 2018 returns Let's learn about Convertible Note SP500 Stocks Performance in 2017

General

Immense Power of Interactive Math Explainers

R/Python